cljmlchapter6-svm

,

在这一章中，我们将会探索支持向量机(SVMs)。我们将会学习多种用Clojure实现支持向量机的方法与原理，并最后利用给定的训练数据建立和训练一个支持向量机。

支持向量机是一种既可以用于解决分类问题也可以用于解决回归问题的监督学习模型。但是在这一章中，我们会把重点放在用支持向量机解决分类问题。支持向量机可以被用于文本挖掘，化学分类以及图像识别和手写字识别。当然，我们需要了解到的事实是，一个机器学习模型性能的好坏很大程度上取决于训练数据的性质以及我们如何调整和优化机器学习模型。

简单的来说，支持向量机利用向量空间中两个类别之间的一个评估得到的最优超平面来分类和预测两个类别的数据。一个超平面比外部的向量空间少一维，比如在一个三维空间中，我们会得到一个二维的超平面。

一个最基本的支持向量机就是一个用于线性分类的非概率模型的二元分类器。但是支持向量机不仅可以解决线性分类问题，还可以用于非线性问题和多分类问题。关于支持向量机一个有趣的事实是支持向量机会在不同类别样本数据之间利用间隔最大化得到一个唯一的分割超平面来划分不同的类别(所谓间隔最大化是指离分割超平面最近的点到分割超平面的距离最大化)。也正是基于这个有趣的特性，支持向量机总是拥有很好的泛化性能并且也实现了自动控制模型复杂度的机制来防止过拟合的发生。因此支持向量机也称作最大间隔分类器。在这一章中我们也会研究相对于其他分类器，支持向量机是如何找到这个最大间隔的。关于支持向量机另一个有趣的事实是，支持向量机可以很好地支持模型特征的扩展，所以支持向量机也经常应用在有大量特征的机器学习问题上。

理解最大间隔分类

如我们之前提到的，支持向量机利用间隔最大化来进行分类，让我们来看看这是如何做到的。首先我们需要引入在第三章中使用的逻辑斯底分类模型作为支持向量机的基础。

在第三章中我们使用逻辑斯底函数或者说是sigmoid函数来对两个不同的类别的输入进行分类。这个函数可以用如下的公式形式化地表示出来，其中表示的是输入的样本数据：

从上面的等式中可以看出，因变量不仅和自变量有关，还和参数有关。其中自变量表示的是模型的输入值向量，表示的是模型中与对应不同特征的权值向量。对于二元分类来说，因变量的值必须在[0, 1]的范围内。最终分类的结果也是看因变量的值是更接近于0还是更接近于1。因此这一项的值如果不是远大于0，就是远小于0。这种关系可以形式化地表达：

如果有N个训练样本，每一个训练样本的输入用表示，输出用表示，我们可以定义损失函数，如下所示：

注意这一项代表了预估模型利用样本输入值计算出来的实际输出值A

对于一个逻辑斯蒂回归模型来说，这一项表示将样本输入传入逻辑斯底函数得到的实际输出值。我们可以继续展开上面等式定义的损失函数中的求和项，如下所示：

很容易就可以发现损失函数的值取决于上面表达式中所示的两个对数项的值。因此，我们可以将损失函数表示成关于这两个对数项的函数，这两个对数项也分别使用和表示，如下所示：

此时虽然要找一个最大间隔但是，但是不同类别样本到分割平面的距离只是限制要大于0，也就是说离分割超平面最近的点到超平面的距离可以为0。这就造成了分类样本点之间会没有分类间隔，而最大间隔分类指的是不仅要将正负示例分开，而且对最难分的实例点也就是离分割超平面最近的点也要有足够大的区分度将它们分到正确的类别中。所以为了提升分类的间隔，我们可以修改hinge-loss函数使得只有当或者时hinge-loss函数的值才大于0。此时的情况可以用公式描述如下：

由于函数间隔对上面的最优化问题的结果并不影响，对目标函数的优化也不影响所以此时可以将代入，并且最大化和最小化等价，所以可以最终得到要求解的最优化问题如下：

由于的取值只有-1和1两种，所以我们就可以得出之前要修改hinge-loss函数使之满足的条件了，也就是只有在有样本点距离分割平面的距离小于最大间隔时，才会增加损失函数的值，说明还需要继续训练。

修改后的hinge-loss函数的变化趋势可以用下面的图表表示，仍然由于的取值只有-1和1两种，所以两种不同类别的样本实际上只会使用到函数或者函数，不会两个函数同时用到。下图所示的是hinge-loss函数对这一类样本的变化趋势图表：

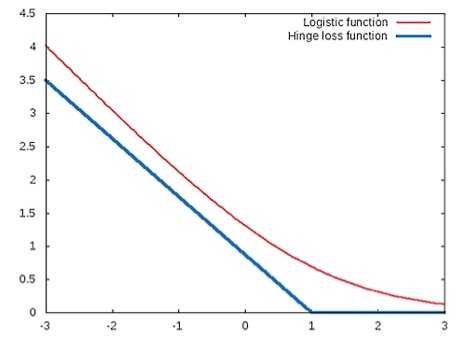
同样的，修改之后的hinge-loss函数对于这一类的样本的变化趋势如下图所示：

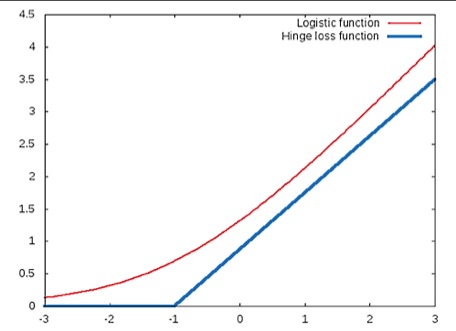
需要注意的是上图中hinge-loss函数的转折点在处。

一个很清晰的结论就是，只有在或者时，也就是样本点距离分割超平面的距离都至少为最大间隔，此时训练的损失值都是0，损失函数不会增大，而在或者时损失值才为正值，此时会增大损失函数的值，说明还需要继续训练我们的支持向量机，从而使得最终的损失函数可以尽可能的小甚至接近于0。

假如我们使用hinge-loss函数来取代函数和函数。那我们就要面对一个支持向量机中的优化问题(更多信息可以参考”Support-vector networks”这篇论文)。这个优化问题可以使用下面公式形式化描述：

在上面的等式中，这一项是正则化项的正则化系数。当，那么支持向量机的行为更多地会受到函数的影响，相反的当时，支持向量机的行为则更多的会受到函数的影响。在某些情况下，正则化系数可以以常数C的形式加入到这个最优化问题中，其中常数C为。此时表达最优化问题的公式变为如下形式：

由于我们只是面对一个二分类问题，的取值为0或者1，我们可以重写上面的最优化问题使之表述起来更为精简优雅，如下所示：

让我们试着可视化出支持向量机在一些训练数据上的行为。假设我们的数据用两个特征维度与。这些训练数据点可以用下面的图标描述：

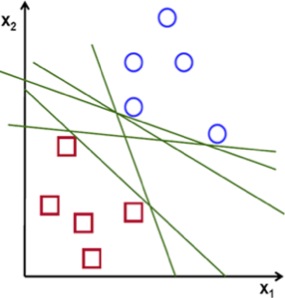
在上面的图表中，分别使用方块和圆圈来表示两个类别的样本数据点。一个线性分类器会试图用上图中所画的许多直线中的一条直线作为决策边界来将图中的样本点分类到两个独立的类别中。当然这个定制的模型不仅需要尽可能地减小总误差，而且还不能让模型对训练数据过拟合要保证有较好的泛化能力。和其他的分类模型一样，支持向量机也会尽可能地将样本数据分类到两个类别中。然后不同的是，支持向量机会在两类输入样本点中确定一个分割超平面，而两个类别中离最终确定的分割超平面的距离将会尽量最大化。这样对于最难以区分的点也有很强的分类能力，可以保证支持向量机的泛化性能。支持向量机的这种行为可以用下面的图标形象的表示出来：

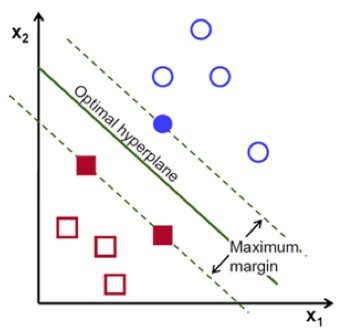
如上图所示，支持向量机会使用两个类之间的最大间隔来确定一个合适的超平面来对两个类别的数据样本进行分类。对于之前提到的这个最优的分割超平面，我们可以用一个等式来形式化的描述，如下所示：

注意在上面的等式中，这一个常数表示的是分割超平面Y轴的截距值。

为了更深入地理解支持向量机是如何获得最大间隔分割平面的，我们需要使用一些基本的向量运算。首先，我们来定义一个给定向量的模长：

在描述支持向量机时还有一种常用的向量运算操作是计算两个向量的内积。计算两个向量的内积可以形式化地表述如下：

需要注意的是，只有当两个向量含有的元素个数相同时才能计算这两个向量的内积。

从上面的等式中可以看到，向量U和向量V的内积的值和向量U的转置与向量V的乘积的值是相同的。此外我们还可以通过一个向量投影到另一个向量的角度来理解两个向量的内积：

需要注意到这一项等于向量U的转置与向量V的乘积。并且与向量的点积相同，我们可以从输入值向量在权值向量方向上投影的角度来重新描述之前提到的最优化问题，可以形式化地表达如下：

因此，训练支持向量机的过程是尽可能最小化权值向量中所有元素的平方和，并且保证用来对两个类别分类的最优分割平面在和两个平面之间。这两个平面称为支持向量机的支持向量。因为我们需要尽可能地减小权值向量的模长，所以投影的大小要尽可能的大，从而保证满足

这两个条件，从而又如下推论：

因此，支持向量机需要保证输入向量在权值向量上的投影尽可能大。这使得支持向量机可以找到训练数据集中两个不同类别样本点之间的最大间隔。

最终支持向量机的分割超平面的为：

而支持向量机的分类决策函数为：

支持向量机的其他形式

现在我们将会接触支持向量机的一些其他形式。如果对这些形式不感兴趣，完全可以跳过本节的内容，完全不会影响后面内容的阅读。但是还是建议读者了解一下这些形式，因为这些形式在支持向量机理论中也是被广泛使用的。

假如垂直于支持向量机评估出来的分类超平面，也就是在超平面的法向方向上，那么我们可以使用如下所示的等式来形式化地描述这个分类用的超平面：

需要注意的是，在上面的等式中，这一项表示超平面在y轴上的截距值，和我们之前用于描述超平面的等式中的这一项类似。

超平面两边的支持向量也可以用如下的等式形式化描述：

现在我们可以利用这一个表达式来确定给定输入样本的类别。假如这个表达式的值小于等于-1，那么我们就可以认为输入的样本属于第一个类别，同样的假如表达式的值大于等于1，那么输入样本的类别就被预测为是属于第二个类别。这个行文可以形式化地描述，如下所示：

上面所使用的两个不等式其实可以变换为一种更简洁的形式，只是用一个不等式来描述：

因此我们可以用一种更简洁的形式来描述支持向量机要解决的最优化问题，如下所示：

在上面描述的约束最优化问题中，我们使用了代替了权值向量。如果使用拉格朗日乘子，我们就可以用如下形式描述要解决的约束最优化问题：

上面所示的最优化问题的形式是支持向量机要解决的最优化问题的原始形式。注意在实践中，只有很少一部分的拉格朗日乘子的值会大于0。此外，这个原始问题还可以表示为输入向量和输出值的线性组合：

因此我们可以将原来的优化问题表示成其对偶形式，同样也是一个约束优化问题，可以形式化地描述：

在上述形式描述的约束优化问题中函数也被称为核函数(kernel function)，我们将会在之后的章节中介绍和讨论这个函数在支持向量机中扮演的角色。

此时将条件代入，可以得到分割超平面为：

分类决策函数变为：

使用支持向量机进行线性分类

正如我们之前介绍的，支持向量机可以对两个独立的类别进行先行分类。支持向量机会试图去寻找一个超平面来分割两个类别的样本点，而这个预估的超平面也描述了我们模型中两个类别之间的最大间距。

比如说，一个在两个类别样本数据之间的预估的超平面可以用下面的图表来可视化地描述：

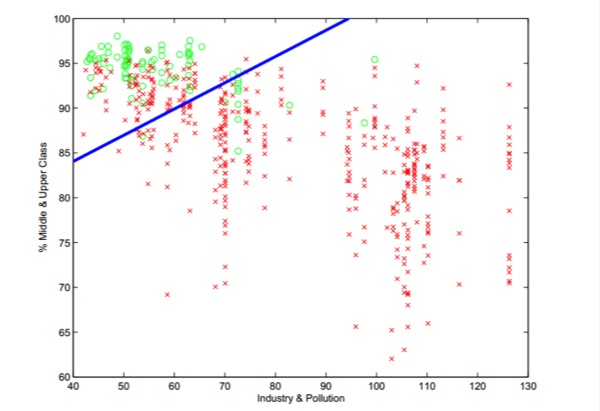
如上面的图标所示，圆圈和十字用来表示样本数据中两个不同类别的样本输入值。而直线就代表了支持向量机的预估超平面了。

在实践中，使用一个已经实现好的经过很多实际项目考验的支持向量机比我们自己实现一个支持向量机要高效和准确的多。现在已经有好多库中实现了支持向量机，并且都提供了多个语言的接口。其中一个库便是LibLinear(http://www.csie.ntu.edu.tw/~cjlin/liblinear/)，这个库中实现了使用支持向量机理论的现行分类器。`clj-liblinear`(https://github.com/lynaghk/clj-liblinear)这个库是Clojure对LibLinear库的一个封装，我们可以利用`clj-liblinear`这个库来很方便得使用Clojure建立一个利用支持向量机理论实现的线性分类器。

要将clj-liblinear库加入到Leiningen项目中，只要在project.clj文件中加上这个库的依赖，如下所示：

[clj-liblinear “0.1.0”]

对于后面我们要实现的例子，需要修改我们项目文件中的名字空间声明，如下所示：

(ns my-namespace

  (:use [clj-liblinear.core :only [train predict]]))

首先让我们来生成一些训练数据，这样我们就可以有属于两个类别的输入数据值了。在这一章的例子中我们将会对两类输入数据进行建模，生成训练数据代码如下所示：

1
2
3
4
5
6
7
8
9
10
(def training-data
  (concat
   (repeatedly
    500 #(hash-map :class 0
                   :data {:x (rand)
                          :y (rand)}))
   (repeatedly
    500 #(hash-map :class 1
                   :data {:x (- (rand))
                          :y (- (rand))}))))

在上面的代码中，我们使用repeatedly函数来生成两个序列，其中每一个序列中的每一个元素都是map对象。每一个map对象中有两个键:class和:data。:class键对应的值表示的是训练输入数据对应的真实类别，:data键对应的值是一个有:x和:y两个键的map对象，这两个键对应的值表示我们训练数据中每一个样本输入的两个特征维度的值，在我们的例子中这些特征值是使用rand函数来随机产生的。最终产生的训练数据中假如某一个样本中两个特征值都是正值，那么这个样本的类别是0，如果两个特征值都是负值，那么这个样本的类别是1。如上面代码所示我们使用repeatedly函数为两个类别分别生成了一个含有500个样本的序列，然后使用concat函数将这两个序列连成一个有1000个元素的序列。我们可以在REPL中查看这些样本输入数据，如下所示：

1
2
3
4
5
6
user> (first training-data)
{:class 0,
:data {:x 0.054125811753944264, :y 0.23575052637986382}}
user> (last training-data)
{:class 1,
:data {:x -0.8067872409710037, :y -0.6395480020409928}}

我们可以使用已经生成的训练数据来创建并且训练一个支持向量机。为了做到这一点，我们需要使用train函数。train函数接受两个参数，第一个参数是一个包含所有训练样本输入值的序列，第二个参数是一个包含所有期望输出值的序列。这两个序列都要保证其中相同位置的元素是对应于训练数据集中的同一个样本，也就是顺序要相同。为了达到分类的目的，期望输出值需要置为给定样本输入值对应的实际类别，如下面代码所示：

1
2
3
4
(defn train-svm []
  (train
   (map :data training-data)
   (map :class training-data)))

上面代码中定义的train-svm函数会利用training-data序列来创建和训练一个支持向量机。现在我们可以使用训练好的支持向量机和predict函数来进行分类了，如下面代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
user> (def svm (train-svm))
#'user/svm
user> (predict svm {:x 0.5 :y 0.5})
0.0
user> (predict svm {:x -0.5 :y 0.5})
0.0
user> (predict svm {:x -0.4 :y 0.4})
0.0
user> (predict svm {:x -0.4 :y -0.4})
1.0
user> (predict svm {:x 0.5 :y -0.5})
1.0

predict函数需要两个参数，第一个参数是一个支持向量机的实例，第二个参数是待分类样本的特征值。

如上面代码所示，我们使用svm变量来表示一个训练好的支持向量机实例。然后我们将svm这个变量和一组类别待预测的样本特征一起传入到predict函数中。可以根据上面代码执行的结果观察到predict函数的输出结果与训练数据集中的实际类别一致。有趣的是，只要输入样本中:y键对应的值大于0，那么分类器分类的结果就认为这个样本属于类别0，相反的如果:y键对应的值小于0，分类器就认为这个样本属于类别1。

在上面的例子中，我们使用了支持向量机来实现分类，无论什么输入训练后的支持向量机的输出值总是一个数字。因此我们还可以用类似上面例子的代码差不多的方法来使用clj-liblinear库来训练一个回归模型。

clj-liblinear这个库还为支持向量机支持了更为复杂的特征类型，比如vectors，maps和sets。现在演示如何使用sets类型的样本输入值来训练一个支持向量机分类器，而不只是像之前例子中的代码一样样本输入值是数字。设想我们现在有从Twitter订阅的给定用户的推文数据流，并且用户已经手动将这些推文分类到了从一个预定义的类别集中选择出来的特定的类别中。这个已经处理好的推文序列可以用如下代码表示：

1
2
3
4
5
6
7
8
9
10
11
12
(def tweets
  [{:class 0 :text "new lisp project released"}
   {:class 0 :text "try out this emacs package for common lisp"}
   {:class 0 :text "a tutorial on guile scheme"}

   {:class 1 :text "update in javascript library"}
   {:class 1 :text "node.js packages are now supported"}
   {:class 1 :text "check out this jquery plugin"}

   {:class 2 :text "linux kernel news"}
   {:class 2 :text "unix man pages"}
   {:class 2 :text "more about linux software"}])

上面代码定义的推文向量中包含有好多个map对象，每一个map对象都有:class和:text两个键。:text这个键对应的值是某一条推文的内容，之后我们就会用这些推文的内容来训练支持向量机。但是我们不能逐字地使用这些推文，因为这些推文中可能会有一些单词是重复的，此外我们还需要用一些方法来解决推文中字母的大小写问题。让我们来定义一个函数将一条推文转化为一个集合(set)，如下代码所示：

1
2
3
4
5
(defn extract-words [text]
  (->> #" "
       (split text)
       (map lower-case)
       (into #{})))

上面代码中定义的extract-words函数会将用text参数表示的字符串转换为一个全是小写字母组成的单词的集合。为了创建一个集合(set)，我们使用(into #{})这个形式。根据Clojure中set的定义，我们得到的集合中将不会有重复的值。需要注意的是我们在extract-words函数中使用了->>这个穿线宏。

在extract-words函数中，使用->>宏在编译器展开的形式可以等同如下的代码形式：

(into #{}

  (map lower-case

    (split text #” “)))

我们可以在REPL中查看extract-words函数的行为，如下所示：

1
2
user> (extract-words "Some text to extract some words")
#{"extract" "words" "text" "some" "to"}

使用extract-words函数，我们就可以有效的利用一个字符串的集合来作为特征值从而训练支持向量机了。如之前提到的，可以使用train函数来做到，如下面代码所示：

1
2
3
4
5
(defn train-svm []
  (train (->> tweets
              (map :text)
              (map extract-words))
         (map :class tweets)))

上面代码定义的train-svm函数首先利用extract-words来处理推文内容从而得到训练输入数据，然后利用train函数来创建并且训练一个支持向量机。现在我们需要组合predict函数和extract-words函数，从而来预测一个待分类的推文的类别，如下面代码所示：

1
2
3
(defn predict-svm [svm text]
  (predict
    svm (extract-words text)))

上面代码所定义的predict-svm函数可以对一个给定的推文进行分类，我们可以在REPL中使用任意的推文内容数据来验证支持向量机预测得到的类别结果，如下所示：

1
2
3
4
5
6
7
8
user> (def svm (train-svm))
#'user/svm
user> (predict-svm svm "a common lisp tutorial")
0.0
user> (predict-svm svm "new javascript library")
1.0
user> (predict-svm svm "new linux kernel update")
2.0

总的来说，clj-liblinear库让我们可以很容易地利用大部分的Clojure数据类型来构建和训练一个支持向量机。而使用这个库的唯一限制就是就是训练模型时输入的含有不同类型的样本集是要能线性可分的。我们将会在本章剩下的章节中学习构建更加复杂的分类器。

使用核支持向量机

在一些情况下，给定的训练数据并不是线性可分的，我们也无法使用线性分类器对训练数据进行建模。因此我们需要使用其他的模型来拟合非线性数据。正如在第四章中描述的那样，人工神经网络可以用来对这一类的样本数据进行建模。在这一节中，我们会描述如何使用核函数(kernel function)来使得支持向量机可以拟合非线性数据。一个使用了核函数的支持向量机也叫做核支持向量机。需要注意的是在本节中提到的支持向量机就是核支持向量机。一个核支持向量机会使用一个非线性的决策边界来分类数据，而这个非线性的决策边界的性质取决于核支持向量机使用的核函数。为了直观地描述这种分类行为，如下图所示就描述了一个支持向量机用一个非线性的决策边界来对两类线性不可分的数据点进行了划分：

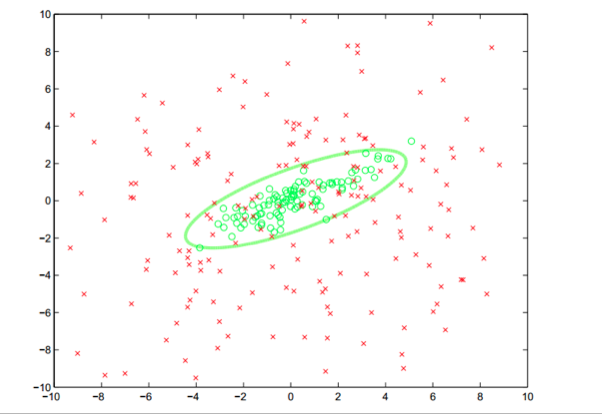
支持向量机中使用的核函数的概念完全是基于数学变换。核函数在支持向量机中的作用是将样本线性不可分的样本数据点进行坐标变换，从而将每一个样本点映射到另一个特征空间(希尔伯特空间)，而在那个样本空间下训练样本数据点是线性可分的。在利用支持向量机进行线性分类的时候是基于样本数据之间的最大间隔。而在分类线性不可分的数据样本时这个最大间隔依然可见。

核函数写作，其中表示的是原本训练数据集中样本的输入值向量，表示经过坐标变换之后映射到其他特征空间之后的输入向量。这个函数表示的是这两个向量在变换后的特征空间的相似程度，可以表示成这两个向量在变换后的特征空间中的内积的大小。假如输入向量有一个给定的类别，而另一个特征空间中的向量在经过线性分类之后也被分到了相同的类别，那么这两个向量的核函数大小将会接近于1，也就是。

一个核函数可以用下面的数学表达式形式化地表述：

在上面的等式中，函数表示从特征空间经过坐标变换到特征空间的映射关系。使用核函数的时候，在学习预测的时候只需要定义核函数，而不用显示地定义映射函数和特征空间，由于特征空间映射关系并不唯一，所以两者都被隐式地包含在了核函数的表达式中。尽管在对给定的训练数据进行建模时可以使用任意的核函数，但是我们必须选择一个核函数来尽可能地减小支持向量机损失函数值的大小。在选取核函数解决实际问题时，通常采用的方法有：一是利用专家的先验知识预先选定核函数；二是采用Cross-Validation方法，即在进行核函数选取时，分别试用不同的核函数，归纳误差最小的核函数就是最好的核函数。

支持向量机中一种常用的核函数是多项式核函数(polynomial kernel function或者polynomic kernel function)，是利用原始特征变量的高阶多项式来对训练数据进行建模。可以回忆我们在第五章中讨论的内容，使用原始特征的多项式作为一个新的特征加入到模型中有时候可以显著提升给定机器学习模型的性能。多项式核函数可以认为是这种思想概念在支持向量机模型上的一种衍生和扩展。这个核函数可以形式化地表述如下：

在上面的等式中，这一项表示多项式特征的最高阶次。此外，当常数项时，这个核函数也被称为是同质(homogenous)的。

另一个广泛使用的核函数是高斯核函数(Gaussian kernel function)。如果对于线性代数很熟练的读着相信对高斯函数应该不会陌生。重要的是要知道，这个函数描述的是一种数据点更接近数据平均值的概率分布，也称正态分布。

在支持向量机中，一般是给定的训练样本集中有两类数据，有一类的样本数据点非常集中也就是每一个样本的每一维特征的值都接近于那一维特征的平均值，而另一类的样本数据的分布则不需要满足这个性质，本节一开始所示的图就是一个很好的例子，圆圈所代表的样本点分布非常集中，而十字代表的样本数据点则很分散，这种情况下就可以使用高斯核函数。高斯核函数的形式化定义如下所示：

在上面等式定义的高斯核函数中，这一项代表训练数据的标准差，也表示高斯核函数的宽度，这个宽度值一般也是利用经验值或者是交叉验证的方法来选取一个相对最优的值代入。

另一种非常流行的核函数是字符串核函数(string kernel function)。核函数不仅可以定义在欧式空间上，还可以定义在离散数据的集合上。字符串核函数就是这样一类核函数，字符串核函数是定义在离散的字符串集合上的核函数。这里所说的字符串是指一个有限长度的字符序列。字符串核函数本质上是在计算两个给定字符串之间的相似度。假如传递给字符串核函数的两个字符串完全相同，那么这个函数返回的值将会是1。因此，当训练数据集中样本中的特征是使用字符串来表示的，那么在使用支持向量机对这个数据集进行建模时字符串核函数将会非常有用。

序列最小最优化算法

支持向量机中的最优化问题可以使用序列最小最优化算法(SMO)来解决。支持向量机要解决的最优化问题是求解一个跨越多个维度的损失函数的数值最优化问题(实质是求解一个凸二次规划问题，并且这个凸二次规划问题存在全局最优解)，从而使得训练后的支持向量机的总误差可以尽可能地达到最小。在实践中，这往往需要用到一些数值优化技术。对于SMO算法的完整讨论与推导已经超出了本书的范围，然后读着需要了解的是，SMO算法是一种使用了分治思想的启发式算法，能够在较短的时间内解决支持向量机需要解决的最优化问题。因为支持向量机要解决的最优化问题中可训练的参数是多维的，比较难以有效地训练，SMO算法本质上是将这个多维的优化问题转变为解决多个二维的最优化问题，每一个子问题中只选取两个变量固定其他的变量，针对选取的两个变量构建一个二次规划问题，此时这个二次规划问题关于选定的两个变量的解应该更接近于原始的二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小，此时这个子问题是可以通过解析方法计算求解，使用SMO算法大大提高了求解最优化问题的速度(更多信息可以参考”Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines”这篇论文)。

LibSVM是一个实现了SMO算法用于训练支持向量机的一个很流行的机器学习库。svm-clj库是一个Clojure对LibSVM库的一个封装，我们将会探索如何使用svm-clj这个库来创建和训练我们的支持向量机模型。

要在Leiningen项目中使用svm-clj这个库，我们需要在project.clj文件中加入这个库的依赖：

[svm-clj “0.1.3”]

在下面的例子中，也需要修改对应文件的名字空间声明，来引入svm-clj库：

(ns my-namespace

  (:use svm.core))

本节的例子中，将会使用一个精简版本的SPECT Heart数据集(http://archive.ics.uci.edu/ml/datasets/SPECT+Heart)。这个数据集描述了几个心脏疾病患者的诊断结果，其中诊断结果是**单质子发射计算机断层扫描(SPECT)**图像。原始数据集中含有267个样本，每一个样本有23个特征。每一个样本的输出值表示了对应病人的诊断结果是阴性还是阳性，其中+1表示诊断结果为阳性，-1表示诊断结果为阴性。

在这个例子中，训练数据存储在项目中的features.dat文件中，这个文件放在Leiningen项目根路径下的resources/路径中，从而方便我们从Clojure代码中获取其中的训练数据。这个文件中包含了多组输入特征值以及某一组输入特征对应的实际类别。让我们来看一下某一条样本数据的形式，如下所示：

1
2
+1 2:1 3:1 4:-0.132075 5:-0.648402 6:1 7:1 8:0.282443 9:1 10:0.5 11:1
12:-1 13:1

如上面所示，一条样本数据中第一个值表示的是这个样本属于的类别值。之后就以键:值的形式存储对应特征的下标号以及这一特征维度的值，可以看到假如特征值是0，那么就可以省略掉这一个特征，比如在上例中就没有用到1:键对应的特征。从上面的例子中还可以很清楚地看到每一个样本最多只有13个特征，训练数据集中每一个样本都使用如上例子所描述格式来存储，这也是要使用LibSVM需要遵守的数据格式。

我们现在可以使用features.dat文件中的样本数据来训练支持向量机了。为了做到这一点，我们使用svm-clj库中的train-model这个函数。此外，由于我们需要先把样本数据从磁盘上载入到内存中，我们需要先调用read-dataset函数，如下面代码所示：

1
2
3
(def dataset (read-dataset "resources/features.dat"))

(def model (train-model dataset))

在上面代码中用model变量表示的训练好之后的支持向量机就可以被用来预测一组给定输入特征值的类别了。predict函数可以帮助我们来进行分类预测。简单起见，我们就使用原始数据集中的样本来进行模型的测试，就不再构造新的样本数据了：

1
2
3
4
5
6
7
8
9
user> (def feature (last (first dataset)))
#'user/feature
user> feature
{1 0.708333, 2 1.0, 3 1.0, 4 -0.320755, 5 -0.105023,
6 -1.0, 7 1.0, 8 -0.4198, 9 -1.0, 10 -0.2258, 12 1.0, 13 -1.0}
user> (feature 1)
0.708333
user> (predict model feature)
1.0

如上面在REPL中看到的结果所示，dataset变量可以看成是一个向量的序列，其中每一个向量第一个值表示一个样本的真实类别，第二个值是一个map对象，在map对象中的键表示特征的下标值，值即为对应的特征值。因为feature变量是一个map对象，所以我们可以将这个符号当做一个函数来调用，如上面代码所示，用(feature 1)来获得feature中1这个键对应的值。

在上面演示的例子中，最终预测的类别和输入样本对应的实际的类别吻合，在这一个例子中支持向量机正确分类给定的一组特征输入值。总的来说，svm-clj这个库让我们可以很方便地构建并训练支持向量机，并且使用训练好的支持向量机来进行分类预测。

使用核函数

如我们之前提到的，当我们需要使用支持向量机拟合非线性可分数据的时候，我们可以选择一个核函数。现在演示在实践中如何借助clj-ml库来构建核支持向量机从而对非线性可分数据进行建模。因为在之前的章节中已经介绍并讨论过这个库了，所以不会再研究如何完整地构建并训练一个支持向量机，而是着重演示如何创建一个使用核函数的支持向量机。

在下面的例子中，因为需要引入clj-ml库，所以我们需要修改一下代码中名字空间的声明：

(ns my-namespace

  (:use [clj-ml classifiers kernel-functions]))

clj-ml.kernel-functions名字空间下的make-kernel-function函数可以用来创建给支持向量机使用的核函数。例如我们可以向这个函数传入:polynomic关键字来创建一个多项式核函数，如下面代码所示：

1
(def K (make-kernel-function :polynomic {:exponent 3}))

如上面代码所示，用K变量表示的多项式核函数的阶次是3。同样的，我们也可以将:string关键字传入make-kernel-function函数来创建一个字符串核函数，如下面代码所示：

1
(def K (make-kernel-function :string))

clj-ml这个库还提供一些其他的核函数的实现，感兴趣的读者可以一一尝试这些核函数的优劣。这个名字空间的文档地址也是在web上公开的http://antoniogarrote.github.io/clj-ml/clj-ml.kernel-functions-api.html。我们可以将`:support-vector-machine`关键字传入`make-classifier`函数从而制定生成的分类器类型是支持向量机，此外还要传入`:smo`关键字来指定是使用SMO算法来训练支持向量机模型，最后需要传入`:kernel-function`关键字来指定生成的支持向量机使用核函数，并且还要传入一个核函数的实例变量，如下面代码所示：

1
2
3
(def classifier
  (make-classifier :support-vector-machine :smo
                   :kernel-function K))

现在我们就有了一个用classifier变量绑定的创建好的支持向量机，之后就可以使用在之前章节中学习到的clj-ml库的使用方法来训练这个支持向量机并用其来进行分类预测。因此，clj-ml这个库让我们很容易地就能创建使用给定核函数的支持向量机。

本章概要

这一章中，我们探索了支持向量机模型，并且讨论了如何用支持向量机来拟合线性可分数据与非线性可分数据。以下是本章内容的几点总结：

  • 介绍了支持向量机是如何利用最大间隔来解决分类问题，以及介绍了支持向量机要解决的最优化问题的一些其他表示形式。
  • 讨论了如何使用核函数来让支持向量机具有分割线性不可分数据的能力，以及使用SMO算法来训练一个支持向量机。
  • 演示了如何使用几个Clojure的库来创建并且训练一个支持向量机并利用其来进行分类预测。

在下一个章节中我们将会把注意力转移到非监督学习问题上，并且会探索一些聚类技术从而可以对这一类机器学习问题进行建模。