cljmlchapter7-clustering data

,

在这一章中我们将把我们的注意力集中在非监督学习(unsupervised learning)问题上。我们会学习几个聚类(clustering)算法，或者说是聚类器(clusterers)的原理，并使用Clojure实现它们。此外还会展示几个已经完整实现了聚类算法的Clojure库。直到本章的最后，我们将会探究降维(dimensionality reduction)技术，以及如何使用这种技术来对给定的高维样本数据提供一个易于理解的可视化效果。

聚类或者说聚类技术(cluster analysis)是一种将数据或者样本进行分组的基本方法。作为一种非监督学习的形式，一个聚类模型使用无标记的数据来进行训练，意味着训练数据中的样本不会带有输入特征值序列对应的类别，训练数据中对于给定的一组输入值并没有描述对应的输出值。一个聚类模型必须确定多组输入特征值之间的相似性，然后自动推断出每一个样本最可能属于的类别。因此使用这一类模型可以将样本数据分成多个群体(簇)。

在解决现实世界中的问题时聚类技术也有若干实际应用。聚类通常被用于图像分析，图像分割，软件演化系统以及社交网络分析。此外聚类不仅广泛应用在计算机科学领域，在生物学分析，基因分析以及犯罪分析等领域也有广泛的应用。

到目前为止已经有好几种聚类算法已经公开并广泛应用在学术界与工业界。而每一种算法都有一组独立的概念，来定义一个簇以及如何将不同的样本组合成一个新的簇。但是不幸的是，目前并没有一种直接的指导方案来描述对于给定的数据集应该用哪一种聚类算法去建模，需要将选定的几个聚类算法作用在数据集上进行试验并计算误差来进行评估，以确定使用一种最合适的聚类算法来聚类给定的样本数据。

这是因为在聚类问题中输入的数据是无标记的，也就是说在输入数据中并没有标出样本对应的类别，也无法使用简单的基于是/否奖励机制的训练来推断出样本属于的类别。

在这一章中，我们将会了解少数的几个可以用在非标记数据集上的聚类技术。

使用K-means聚类

K-means聚类算法是一种基于矢量量化的聚类技术(更多信息可以参考”Algorithm AS 136: A K-Means Clustering Algorithm”这篇论文)。这个算法将一系列的以向量形式表示的样本分成K个样本簇，所以也因此而得名。在这一章中我们将学习K-means算法的性质，并且尝试将其实现。

矢量量化(Vector Quantization)技术通常用于信号处理领域，用来将一个包含很多值的大集合中的值映射到一个只含有少量值的空间中的值。例如，一个模拟信号用8位的数字信号来量化，那么可以这个模拟信号中可能有256个不同的量化等级，也就是有256个值。而假如需要将原本上的值映射到的范围内，一个简单的做法就是将原本的信号值乘上，从而将信号值映射到新的范围内。在聚类的情境中，对输入数据或者输出数据进行矢量量化可行的原因如下：

  • 可以将聚类行为限制到一个有限的集簇内。
  • 在聚类过程中需要适应在一定范围内的样本数据并不会每次都聚集到同一个簇中，而这种灵活性决定了聚类算法可以对没有对应类别的样本值进行分组。

这个算法的要点可以简单地概括如下。这个K个均值点，或者说重心点，一开始是被随机选择出来的。然后计算除了选出的重心点以外的所有样本点到这几个重心点的距离。然后一个样本点将被分组到离这个样本点最近的重心点代表的簇中。在一个多维空间中，每一个样本数据都有多个维度的特征值，将使用欧式距离(Euclidean distance)来计算各个输入向量到给定的重心点，这一步在K-means算法中称作分配步骤。

K-means算法中的下一步称为更新步骤。此时K个重心点的坐标位置不再是一开始随机选出的坐标值，而是利用之前分组之后的每一簇中的所有样本点坐标值平均值来作为新的重心点的坐标值。然后重复迭代这两部操作，直到在相邻的两次更新中重心坐标的偏移量基本可以忽略不计。因此这个算法的最终结果是给定的训练数据中每一组输入特征值都被分到一个簇，或者说一个类别中。

K-means算法的迭代过程可以用下面的一组图来可视化地展示：

上面组图中的每一张图都表示了K-means算法对于给定训练数据在每一次迭代后重心的坐标位置以及其余样本的分组情况。最后一张图表示了最后一次迭代之后K-means算法聚类出的不同簇的位置。

K-means聚类算法的优化目标可以用如下表达式形式化地描述：

在上面表达式中定义的最优化问题中，这几项代表了用来聚类输入值的簇的重心坐标值。K-means算法可以最小化每一个簇的大小，同时也确定了每一个簇的重心位置。

这个算法需要个样本数据以及个初始的随机均值点作为算法的输入。在最开始的分配步骤中，输入样本值被分配到以传给算法的初始随机均值点为重心位置的簇中。在之后的更新步骤中，利用初始聚类的样本数据来计算每一个簇的新的重心位置。在大部分的K-means算法的实现中，都是利用某一个簇中所有样本点坐标的均值来作为这个簇新的重心位置。

大多数的K-means算法实现中都是从训练数据集中随机的选择个样本点最为初识情况下的个簇的重心点。这种技术也称作Forgy随机初始化方法。

假如要聚类的簇的个数是无限大的或者输入样本数据中的特征维度是无限大的，那么K-means算法是一个NP-hard问题。当这两个值都确定了边界范围之后，K-means算法的时间复杂度是。根据计算新的均值的方法不同，K-means算法还有几个不同的变种。

现在将会演示如何不使用额外的依赖库，只是用简单的Clojure代码来实现K-means算法。我们会先定义这个算法的所有细节和小模块，然后将这些小模块组合在一起从而得到一个基本的K-means算法。

两个数字之间的距离可以被定义为这两个数字的值差值的绝对值，我们可以实现一个distance函数来计算两个数的距离，如下面代码所示：

1
2
(defn distance [a b]
  (if (< a b) (- b a) (- a b)))

假如我们给定一组平均值，我们可以计算出哪一个平均值离给定的数字最近，我们可以利用distance函数和sort-by函数来做到这一点，如下面代码所示：

1
2
(defn closest [point means distance]
  (first (sort-by #(distance % point) means)))

为了演示如何使用上面代码定义的closest函数，我首先需要定义一些样本数据放在一个序列中表示，然后再定义一些均值也同样放在序列中表示，如下面代码所示：

1
2
(def data '(2 3 5 6 10 11 100 101 102))
(def guessed-means '(0 10))

现在我们可以在REPL中将任意数字和guessed-means变量传入closest函数，从而检查closest函数的行为：

1
2
3
4
5
6
user> (closest 2 guessed-means distance)
0
user> (closest 9 guessed-means distance)
10
user> (closest 100 guessed-means distance)
10

我们给定的均值是0和10，所以将2传入后closest函数会返回距离2最近的均值0，而将9和100传入则会返回距离这两个给定数值较近的均值10。因此，给定的数据集中的样本数据可以被分组到距离最近的均值对应的簇中。我们可以使用closest函数和group-by函数来实现一个函数来执行分组的行为，如下面代码所示：

1
2
(defn point-groups [means data distance]
  (group-by #(closest % means distance) data))

上面代码定义的point-groups函数需要传入三个参数，第一个参数是给定的一组均值，第二个参数是待分组的数据集，最后一个参数是用来计算待分组数据集中样本数据与均值之间距离的函数行为。需要注意的是，在使用group-by函数时需要两个参数，第一个参数是一个函数闭包，第二个参数是一个数据序列，通过将数据序列中的值不断地传入函数闭包中得到计算结果，最终利用得到的计算结果来对数据序列分组。

我们可以将data变量表示的待分组数据集，guessed-means变量表示的均值序列还有用来计算数值距离的distance函数传入point-groups函数，从而对给定的待分组数据集进行简单的聚类，如下面代码所示：

1
2
user> (point-groups guessed-means data distance)
{0 [2 3 5], 10 [6 10 11 100 101 102]}

如上面代码所示，point-groups函数将用data变量表示的待分组数据集划分到了两个组别中。为了计算分出来的两个组别中新的均值，我们可以分别计算每一个组中所有数值的平均值，可以使用reduce函数和count函数来实现这一步操作，如下面代码所示：

1
2
3
(defn average [& list]
  (/ (reduce + list)
     (count list)))

我们会实现一个函数来将上面代码定义的average函数作用在之前的均值序列以及point- groups函数返回的用map对象表示的分组结果上，从而计算每一个分组中新的均值：

1
2
3
4
5
(defn new-means [average point-groups old-means]
  (for [m old-means]
    (if (contains? point-groups m)
      (apply average (get point-groups m))
      m)))

上面代码中定义的new-means函数中，对于每一个之前均值序列中的均值，我们将average函数作用在这个均值对应的簇中的所有样本点组成的序列上。当然在使用average函数之前，我们需要先判断当前选择出来的均值是否出现在之前的分组结果中，也就是这个均值对应的簇中是否有样本数据点，我们new-means函数中使用contains?函数来做这个验证检查。我们可以在REPL中查看new-means函数作用在上一个均值序列以及上一次分组结果后返回的结果值，如下所示：

1
2
3
4
user> (new-means average
           (point-groups guessed-means data distance)
           guessed-means)
(10/3 55)

如上面例子的输出所示，我们利用new-means函数将一开始的均值序列(0 10)变为了新的均值序列(10/3 55)。为了实现K-means算法，我们需要把new-means函数不断地作用在上一次迭代得到的均值序列上。这个迭代过程可以使用iterate函数来实现，其中iterate函数需要传入一个单参数的函数闭包。

我们可以先定义要传给iterate函数的闭包，在这个闭包中，我们将上一次迭代的均值序列传给new-means函数，从而得到新的均值序列。如下面代码所示：

1
2
3
4
(defn iterate-means [data distance average]
  (fn [means]
    (new-means average
               (point-groups means data distance) means)))

上面代码中定义的iterate-means会返回一个新的匿名函数，这个匿名函数接受上一次的均值序列作为参数，然后利用这个匿名函数可以计算出新的均值序列，我们可以在REPL中查看这个返回的结果：

1
2
3
4
user> ((iterate-means data distance average) '(0 10))
(10/3 55)
user> ((iterate-means data distance average) '(10/3 55))
(37/6 101)

从上面的输出结果可以看到，每一次使用iterate-means函数，都可以得到一个新的均值序列，其中iterate-means函数返回匿名函数就可以当做函数闭包传入iterate函数，而iterate函数会返回一个无穷大的包含每一次得到均值序列的序列，所以我们需要使用take函数来查看iterate函数返回的结果，从而查看每一次迭代得到的均值序列，如下面代码所示：

1
2
3
user> (take 4 (iterate (iterate-means data distance average)
                        '(0 10)))
((0 10) (10/3 55) (37/6 101) (37/6 101))

从上面的结果中可以观察到，对于我们给定的训练样本数据，均值序列仅仅在前三次迭代中发生了改变，最终收敛到了(37/6 10)的位置。K-means算法的终止条件是均值序列可以收敛到一个相对稳定的值，因此我们必须不断地将由iterate-means函数生成的函数闭包新生成的均值序列传入函数闭包中做下一次迭代，直到连续的两次迭代过程中得到的均值序列不再改变或者变化的偏差在一个可容忍的范围内。因为iterate函数会惰性地返回一个无穷大的序列，所以我们必须实现一个函数来根据均值序列收敛的位置来限制iterate返回的无穷大惰性序列的长度。我们可以使用lazy-seq函数和seq函数以惰性唤醒的方式来实现这种行为，如下面代码所示：

1
2
3
4
5
6
7
8
9
(defn take-while-unstable
  ([sq] (lazy-seq (if-let [sq (seq sq)]
                    (cons (first sq)
                          (take-while-unstable
                           (rest sq) (first sq))))))
  ([sq last] (lazy-seq (if-let [sq (seq sq)]
                         (if (= (first sq) last)
                           nil
                           (take-while-unstable sq))))))

上面代码定义的take-while-unstable函数将一个惰性序列分割成头部和尾部两部分，然后比较头部元素和尾部第一个元素是否相同，假如两个元素相同，则返回一个空序列或者nil，如果两个元素不相同，就将惰性序列的尾部作为参数递归调用take-while-unstable函数。使用lazy-seq的目的是为了将返回的序列变为惰性的从而可以节省不必要的求值计算，注意到我们还使用了if-let这个宏，这个宏其实就是一个简单的let形式加上一个if表达式，因为假如参数sq是一个空序列的话，那么(seq sq)会返回nil，所以如果使用if-let宏的话可以更优雅简洁的判断是否到了递归的种植条件。我们可以在REPL中查看take-while-unstable函数的行为以及这个函数的输出：

1
2
3
4
5
6
7
user> (take-while-unstable
       '(1 2 3 4 5 6 7 7 7 7))
(1 2 3 4 5 6 7)
user> (take-while-unstable
       (iterate (iterate-means data distance average)
                '(0 10)))
((0 10) (10/3 55) (37/6 101))

使用最终计算得到的均值序列，我们可以使用vals函数从point-groups函数返回的以map对象形式存储的聚类结果中得到每一个簇中所含有的数据样本，如下面代码所示：

1
2
(defn k-cluster [data distance means]
  (vals (point-groups means data distance)))

需要注意的是vals以序列形式返回一个map对象中所有的值。

上面代码定义的k-cluster函数利用K-means算法得到给定输入数据集的最终聚类结果。我们可以将最终迭代得到的均值序列(37/6 101)传入k-cluster函数来得到给定输入数据集的最终聚类结果，如下面代码所示：

1
2
user> (k-cluster data distance '(37/6 101))
([2 3 5 6 10 11] [100 101 102])

为了可以将给定数据集中的样本在聚类过程中聚类结果的变化直观地显示出来，我们可以将k-cluster函数作用在之前定义的由iterate函数和iterate-means函数组成的迭代过程返回的含有每一次迭代的均值序列的结果序列上。此外我们还要利用take-while-unstable函数来判断序列的收敛点从而限制返回序列的长度。整个过程如下面代码所示：

1
2
3
4
5
6
user> (take-while-unstable
          (map #(k-cluster data distance %)
               (iterate (iterate-means data distance average)
                '(0 10))))
(([2 3 5] [6 10 11 100 101 102])
([2 3 5 6 10 11] [100 101 102]))

我们可以将上述代码所示的表达式进行重构为一个函数，这个函数(准确的说是一个闭包)只需要一个参数来表示初识时的均值序列，函数内部中将这个均值序列和待聚类数据集以及用来计算数值之间距离的函数还有计算一个序列中所有值的均值的函数传给iterate-means来进行迭代计算。如下面代码所示：

1
2
3
4
5
6
(defn k-groups [data distance average]
  (fn [guesses]
    (take-while-unstable
     (map #(k-cluster data distance %)
          (iterate (iterate-means data distance average)
                   guesses)))))

我们可以将一开始定义的待聚类数据集以及两个作用在数值变量上的函数distance和average传入上面代码定义的k-groups函数，如下面代码所示：

1
2
(def grouper
  (k-groups data distance average))

现在我们可以把任意的初始均值序列作为参数传给上面代码定义的grouper函数，从而可以看到对不同的初始均值序列，K-means算法在聚类的过程中迭代的次数不同，最终收敛到的均值序列的值也不同，也就是说最后的聚类结果也不同，我们可以在REPL中观察不同初始均值序列下K-means算法聚类的迭代过程，每一次迭代的聚类结果以及最终的聚类结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
user> (grouper '(0 10))
(([2 3 5] [6 10 11 100 101 102])
 ([2 3 5 6 10 11] [100 101 102]))
user> (grouper '(1 2 3))
(([2] [3 5 6 10 11 100 101 102])
 ([2 3 5 6 10 11] [100 101 102])
 ([2 3] [5 6 10 11] [100 101 102])
 ([2 3 5] [6 10 11] [100 101 102])
 ([2 3 5 6] [10 11] [100 101 102]))
user> (grouper '(0 1 2 3 4))
(([2] [3] [5 6 10 11 100 101 102])
 ([2] [3 5 6 10 11] [100 101 102])
 ([2 3] [5 6 10 11] [100 101 102])
 ([2 3 5] [6 10 11] [100 101 102])
 ([2] [3 5 6] [10 11] [100 101 102])
 ([2 3] [5 6] [10 11] [100 101 102]))

正如之前提到的，假如给定的初始均值序列中均值的个数大于待聚类数据集中样本的个数，那么我们最终得到的聚类结果就是，最终聚类得到的簇的个数与待聚类数据集中样本的个数相同，也就是说每一个簇中只有一个样本。我们可以在REPL中用grouper函数验证这一点，如下面代码所示：

1
2
user> (grouper (range 200))
(([2] [3] [100] [5] [101] [6] [102] [10] [11]))

我们可以将之前实现的算法扩展到向量值上，而不只是单单作用于简单的数值上，为了做到这一点我们需要修改作为参数传入k-groups函数的distance函数和average函数。这两个函数扩展到向量空间下的实现如下面代码所示：

1
2
3
4
5
(defn vec-distance [a b]
  (reduce + (map #(* % %) (map - a b))))

(defn vec-average [& list]
  (map #(/ % (count list)) (apply map + list)))

上面代码所定义的vec-distance函数利用计算两个向量对应位置元素的差值并且求取这些差值的平方和的方法实现了求取两个向量的平方欧氏距离。上面代码定义的vec-average函数是将多个向量相加，然后将相加得到的向量中的每一个元素都除以向量的个数的方法来实现求取多个向量的平均值。我们可以在REPL中观察这两个函数的返回值，如下所示：

1
2
3
4
user> (vec-distance [1 2 3] [5 6 7])
48
user> (vec-average  [1 2 3] [5 6 7])
(3 4 5)

现在，可以为我们的聚类算法定义一些向量空间下的值来作为待分类的样本数据集，如下所示：

1
2
(def vector-data
  '([1 2 3] [3 2 1] [100 200 300] [300 200 100] [50 50 50]))

现在我们可以将vector-data变量，以及vec-distance和vec-average两个函数传给k-groups函数，从而可以看到在待聚类样本是在向量空间下时聚类过程中每一次迭代的聚类结果以及最终算法收敛时的聚类结果，如下所示：

1
2
3
4
5
6
7
8
user> ((k-groups vector-data vec-distance vec-average)
       '([1 1 1] [2 2 2] [3 3 3]))
(([[1 2 3] [3 2 1]] [[100 200 300] [300 200 100] [50 50 50]])
 ([[1 2 3] [3 2 1] [50 50 50]]
  [[100 200 300] [300 200 100]])
 ([[1 2 3] [3 2 1]]
  [[100 200 300] [300 200 100]]
  [[50 50 50]]))

对于当前算法的实现中另一个可以改进的点是假如传入给new-means函数的均值序列中含有相同的值我们需要new-means函数每次只更新均值序列中具有相同值的元素中的一个元素的值。现在假如我们向new-means函数中传入一个均值序列，那么如果这个序列中有相同值的元素，这些具有相同值的元素都会被更新。然而，在经典的K-means算法中，每一次更新仅允许更新均值序列中相同值元素中的其中一个值。我们可以在REPL中验证当前算法存在的缺陷，我们向new-means函数传递'(0 0)作为初始的均值序列，如下面代码所示：

1
2
3
4
user> (new-means average
                 (point-groups '(0 0) '(0 1 2 3 4) distance)
                 '(0 0))
(2 2)

我们可以通过检查给定的均值在均值序列中是否重复出现，如果重复出现那么只更新这些具有相同值的均值中的其中一个来避免这个问题。我们可以利用frequencies函数来实现这个功能。frequencies函数接受一个序列，然后统计这个序列中每一个元素重复出现的次数，最后返回一个map对象，这个map对象中的键即为序列中的值，而建对应的值即为序列中每一个值重复出现的次数。因此，我们可以重新定义new-means函数，如下面代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
(defn update-seq [sq f]
  (let [freqs (frequencies sq)]
    (apply concat
           (for [[k v] freqs]
             (if (= v 1)
               (list (f k))
               (cons (f k) (repeat (dec v) k)))))))

(defn new-means [average point-groups old-means]
  (update-seq
   old-means
   (fn [o]
     (if (contains? point-groups o)
       (apply average (get point-groups o)) o))))

上面代码定义的update-seq函数接受一个函数闭包f和一个均值序列sq两个参数。我们可以看到在update-seq函数中定义的行为是假如均值序列中的某一个元素没有重复出现那么就照常更新这个均值，而如果某一个元素重复出现了，那么仅仅更新遍历到的第一个值，余下的相同的值则不做操作。现在可以来观察用重新定义的new-means函数来更新均值序列，假如均值序列中存在重复出现的值那么每次只会更新其中一个，我们依然传入'(0 0)作为初始均值序列，可以在REPL中观察结果，如下所示：

1
2
3
4
user> (new-means average
                 (point-groups '(0 0) '(0 1 2 3 4) distance)
                 '(0 0))
(2 0)

现在我们可以观察利用重新定义后的new-means函数进行聚类的结果。现在不管传入的初始均值序列中是否有重复出现的元素，我们最终都可以得到同样的聚类结果，以'(0 0)，'(0 1)以及'(0 2)为例，我们先来看修改之前的结果：

1
2
3
4
5
6
7
8
9
user> ((k-groups '(0 1 2 3 4) distance average)
       '(0 1))
(([0] [1 2 3 4]) ([0 1] [2 3 4])
user> ((k-groups '(0 1 2 3 4) distance average)
       '(0 0))
(([0 1 2 3 4])
user> ((k-groups '(0 1 2 3 4) distance average)
       '(0 2))
(([0 1] [2 3 4])

而使用修改之后的new-means函数，利用三种初始均值序列来进行聚类后最终都会收敛到同一个聚类结果：

1
2
3
4
5
6
7
8
9
user> ((k-groups '(0 1 2 3 4) distance average)
       '(0 1))
(([0] [1 2 3 4]) ([0 1] [2 3 4]))
user> ((k-groups '(0 1 2 3 4) distance average)
       '(0 0))
(([0 1 2 3 4]) ([0] [1 2 3 4]) ([0 1] [2 3 4]))
user> ((k-groups '(0 1 2 3 4) distance average)
       '(0 2))
(([0 1] [2 3 4]))

重新定义后的new-means函数对于含有重复出现元素的初始均值序列表现出来的行为同样可以扩展到初始均值序列中的元素是向量时的情况，如下所示：

1
2
3
4
5
6
user> ((k-groups vector-data vec-distance vec-average)
       '([1 1 1] [1 1 1] [1 1 1]))
(([[1 2 3] [3 2 1] [100 200 300] [300 200 100] [50 50 50]])
 ([[1 2 3] [3 2 1]] [[100 200 300] [300 200 100] [50 50 50]])
 ([[1 2 3] [3 2 1] [50 50 50]] [[100 200 300] [300 200 100]])
 ([[1 2 3] [3 2 1]] [[100 200 300] [300 200 100]] [[50 50 50]]))

总的来说，上面例子中实现的k-cluster函数和k-groups函数展示了如何用纯Clojure代码来实现一个K-means聚类算法。

使用clj-ml库来聚类数据

clj-ml库是Java机器学习库weka的封装，这个库提供了几种聚类算法的实现。现在来演示如何利用clj-ml库来建立一个K-means聚类器。

要在Leiningen项目中使用clj-ml库和Incanter库，我们需要把这两个库的依赖加入到project.clj文件中：

[cc.artifice/clj-ml “0.4.0”]

[incanter “1.5.4”]

对于下面我们将会实现的例子中，我们需要修改文件中名字空间的定义从而引入两个库中提供的函数：

(ns my-namespace

  (:use [incanter core datasets]

    [clj-ml data clusterers]))

在这一章中使用clj-ml库的例子中，我们将会使用Incanter库中提供的Iris数据集来作为我们的训练数据集。这个数据集本质上是150朵花的数据集，每一朵花的样本数据中，都有四个维度的特征来描述这个样本。其中在数据集中每一个样本的四个特征分别是花瓣的宽度和长度以及花萼的宽度和长度。这一个数据集中花的样本来自三个类别，分别是Virginica，Setosa和Versicolor。这个数据使用大小的矩阵来描述，其中每一朵花属于的种类放在这个矩阵中的最后一列。

我们可以使用Incanter库中的get-dataset函数，sel函数以及to-vector函数从而以向量形式从Iris数据集中提取出所有样本的特征值，如下面代码所示。然后我们可以使用clj-ml库中的make-dataset函数来将之前得到的特征值向量转化为可供clj-ml中聚类函数使用的数据格式。我们还需要向make-dataset函数传入一个表示特征向量解构的模板从而可以让处理函数来解析传入的数据集，此外还要传入一个字符串表示这个生成的数据集的名字，需要注意的是一开始得到的特征值向量其实一个向量的向量，其中每一个元素也是一个向量类型，整个数据生成过程如下面代码所示：

1
2
3
4
5
6
7
8
9
10
(def features [:Sepal.Length
               :Sepal.Width
               :Petal.Length
               :Petal.Width])

(def iris-data (to-vect (sel (get-dataset :iris)
                             :cols features)))

(def iris-dataset
  (make-dataset "iris" features iris-data))

我们可以在REPL中打印出上面代码定义的iris-dataset变量，从而可以观察到最终得到的训练数据集中的内容，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
user> iris-dataset
#<ClojureInstances @relation iris
@attribute Sepal.Length numeric
@attribute Sepal.Width numeric
@attribute Petal.Length numeric
@attribute Petal.Width numeric
@data
5.1,3.5,1.4,0.2
4.9,3,1.4,0.2
4.7,3.2,1.3,0.2
...
4.7,3.2,1.3,0.2
6.2,3.4,5.4,2.3
5.9,3,5.1,1.8>

我们可以利用clj-ml.clusterers名字空间中的make-clusterer函数来创建一个聚类器。我们可以将要生成聚类器的类型作为第一个参数传给make-clusterer函数，而将要生成聚类器时的一些配置参数以map对象形式作为第二个参数传给make-clusterer函数。我们可以使用clj-ml库中的cluster-build函数来训练给定的聚类器。如下面代码所示，我们使用make-cluster函数创建了一个新的聚类器，并且用:k-means关键字作为参数来指定了生成的聚类器的类型，然后定义了train-clusterer函数来帮助我们利用给定的数据集来训练这个新生成的聚类器：

1
2
3
4
5
6
7
(def k-means-clusterer
  (make-clusterer :k-means
                  {:number-clusters 3}))

(defn train-clusterer [clusterer dataset]
  (clusterer-build clusterer dataset)
  clusterer)

我们可以将用k-means-clusterer变量表示的聚类器实例以及用iris-dataset变量表示的训练数据集传入train-clusterer函数从而观察聚类器训练后的结果，如下代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
user> (train-clusterer k-means-clusterer iris-dataset)
#<SimpleKMeans
kMeans
======

Number of iterations: 6
Within cluster sum of squared errors: 6.982216473785234
Missing values globally replaced with mean/mode

Cluster centroids:
                            Cluster#
Attribute       Full Data          0          1          2
                    (150)       (61)       (50)       (39)
==========================================================
Sepal.Length       5.8433     5.8885      5.006     6.8462
Sepal.Width        3.0573     2.7377      3.428     3.0821
Petal.Length        3.758     4.3967      1.462     5.7026
Petal.Width        1.1993      1.418      0.246     2.079

如上面代码的输出结果所示，训练后聚类器的聚类结果中在第一个簇(cluster0)中有61个样本，在第二个簇(cluster1)中有50个样本，而在第三个簇(cluster2)中有39个值。上面的输出结果同样告诉了我们聚类后的三个簇中的每一个簇最后的均值序列的值，也就是最终对给定数据进行聚类之后，每一类中四个特征的平均值。现在我们可以将训练好的聚类器实例传入clj-ml库提供的clusterer-cluster函数中，从而可以对给定的输入样本数据进行类别预测，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
user> (clusterer-cluster k-means-clusterer iris-dataset)
#<ClojureInstances @relation 'clustered iris'
@attribute Sepal.Length numeric
@attribute Sepal.Width numeric
@attribute Petal.Length numeric
@attribute Petal.Width numeric
@attribute class {0,1,2}
@data
5.1,3.5,1.4,0.2,1
4.9,3,1.4,0.2,1
4.7,3.2,1.3,0.2,1
...
6.5,3,5.2,2,2
6.2,3.4,5.4,2.3,2
5.9,3,5.1,1.8,0>

clusterer-cluster函数使用训练好的聚类器实例返回一个新的数据集，在这个新返回的数据集中将会增加一列，表示每一个样本数据在经过聚类之后所分到的类别编号。如上面输出结果所示，这一个新的列中的值为0，1或者2，分别代表了对应这一行的样本属于cluster0，cluster1后者是cluster2。总的来说，clj-ml为我们使用聚类算法提供了一套非常易用的框架，并且在上面的例子中我们使用clj-ml库创建并训练了一个K-means聚类器。

使用层次聚类

层次聚类(Hierarchical clustering)是另一在聚类分析中常用的技术，层次聚类分为自顶向下和自底向上两种，自顶向下的方法是指初始时将数据集中的所有数据对象看做是一个簇，而后根据某些规则逐步细分分成不同的簇，然后递归细分的步骤直到某一终止条件。自底向上的方法是指先把每一对象看做一个簇，使用迭代的方法处理这些簇，在每次迭代中将根据某一规则计算出的最相近的两个簇合并为一个簇，直到簇的数量达到达到指定的值终止算法的执行。自底向上的聚类方法也称为聚集型聚类(agglomerative clustering)，而自顶向下的聚类方法也称为分裂型聚类(divisive clustering)。

因此在聚集型聚类算法中，我们是将多个小的簇来组成一个大的簇，而在分裂型聚类算法中我们是将一个大的簇切分为多个小的簇。在算法性能上，现在常用的聚集型聚类算法的实现一般的时间复杂度为，而分裂型聚类算法的时间复杂度则要高一些，为。

假设在我们的训练数据集中有6个样本，在下面的例子中，使用二维坐标系来描述我们的特征空间，所有的输入样本都是一个二维空间中的点，如下图所示：

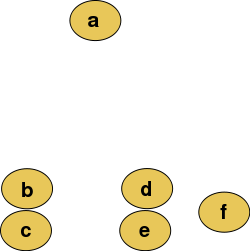
然后我们可以对这些输入样本进行聚集型聚类，最终产生的聚类后的层次结构如下图所示：

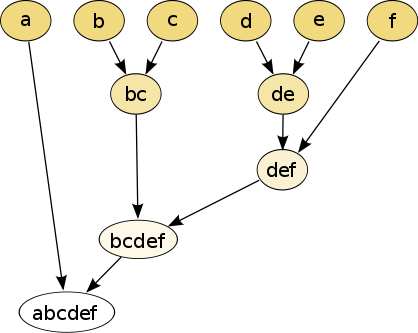
在上图中可以看到样本和样本在当前的空间分布中距离最近，所以这两个样本被分组到了一个簇中。类似的，样本d和样本e也被分组到了另一个簇中。最终这个层次聚类的最终结果是一颗关于输入样本数据的二叉树或者是一个关于输入样本数据的树状图。实际上，像和这样的簇都是作为其他簇的二叉子树的根节点被加入到最终聚类得到的层级结构中。尽管这个处理过程，在对于特征空间是二维空间时相对简单容易，但是如果训练数据集中每一个样本都在一个很高维度的特征空间内，那么这个过程将变得繁琐，因为需要计算在高维特征空间中多个样本点之间的距离。

不论是在聚集型聚类技术还是分裂型聚类技术中，都需要计算训练数据中两两样本点之间的相似度。我们可以计算两两样本输入值的距离来作为相似度的标准，距离最近的两组样本输入值被分组到一个簇中，然后然后重新计算各个簇之间或者样本输入点之间的联动性或者相似度。

层次聚类算法中选择的不同的距离度量方法会决定这个聚类算法最终聚类结束之后各个簇的形状。一组常用的用于确定向量和向量之间距离的度量方法是使用欧氏距离，与平方欧式距离，这两个距离度量函数可以形式化地表述如下：

另一种经常使用的两个输入向量之间的距离计算方法是最大距离，这个方法是依次计算给定的两个向量中每一个对应位置上元素值的差值的绝对值，并取数值最大的绝对值作为这两个向量之间的距离。这个方法也可以形式化地表述如下：

层次聚类算法中另一个很重要的概念是联动标准(linkage criteria)，可以有效的描述和衡量输入样本数据中两个簇之间的相似性或者相异性。常用的用来确定两个输入值的联动性的方法有单点联动聚类(single linkage clustering)和完全联动聚类(complete linkage clustering)，这两种方法都属于聚集型聚类的形式。

在聚集型聚类算法中，两个距离最短的输入样本或者簇会被合并为一个新的簇。当然不同的聚集型聚类算法对于”最短距离”的定义都各不相同。在完全联动聚类方法中，两个簇之间的距离被定义为这两个簇中距离最远的两个样本点之间的距离值。因此这种方法也被称为最远邻聚类(farthest neighbor clustering)。这种计算两个簇之间的距离的度量标准可以形式化地表述如下：

上面等式中的函数表示和这两个向量之间的距离，而计算距离的常见方法我们已经在上文介绍过了。完全联动聚类本质上会利用上述的等式计算各个簇或者输入值之间的距离，然后选择两个距离最短的簇或者输入值合并为一个新的簇，然后重复这个合并过程直到只剩下一个簇。

与完全联动聚类相反，在单点联动聚类中两个簇之间的距离被定义为这两个簇中距离最短的两个样本点之间的距离，因此单点联动聚类也被称为最近邻聚类(nearest neighbor clustering)，可以形式化的表述如下：

另一种很流行的层次聚类技术是Cobweb算法。这个算法是概念聚类(conceptual clustering)的一种形式，在概念聚类中，聚类算法会为每一个生成的簇产生一个概念。这里指的”概念”是一个对某一类数据的精简的格式化描述。有趣的是，概念聚类算法与我们在第三章中讨论过的决策树学习算法非常相似。Cobweb算法将所有的的簇放入到一个分类树中，这颗分类树中的每一个节点存储了这个节点下面子节点的概念或者说是描述信息，而这颗分类树的叶子节点也就代表了聚类之后的簇。我们利用非叶子节点中存储的概念可以对缺失了一些特征值的输入样本的类别进行预测。在这个意义上来说，Cobweb算法这种技术可以被用在测试数据集中有的样本缺少特征值或者存在未知特征值的情况。

现在将演示如何实现一个简单的层级聚类器。在这个实现中，我们会扩展Clojure语言，我们会将一些在本个例子中会需要用到的一些功能嵌入到Clojure语言标准库中的向量数据结构中，也就是我们需要扩展clojure.lang.PersistentVector这个标准库中的数据结构。

对于接下来要做的例子，我们需要clojure.math.numeric-tower库，为了将这个库加入到Leiningen项目中，我们需要在project.clj文件中加入相关的依赖：

[org.clojure/math.numeric-tower “0.0.4”]

同时为了在代码中可以使用这个库中的函数，我们需要修改代码中的名字空间声明，如下所示：

(ns my-namespace

  (:use [clojure.math.numeric-tower :only [sqrt]]))

在本例的实现中，我们会利用欧式距离来计算两个样本点之间的距离。我们可以用reduce函数和map函数来实现一个可以计算某一个序列所有元素平方和的函数从而来实现计算欧式距离。如下代码所示：

1
2
(defn sum-of-squares [coll]
  (reduce + (map * coll coll)))

上面代码中定义的sum-of-squares函数被用来计算样本之间的距离。现在来定义两个协议(protocol)来对我们将要对特定的数据类型进行的操作进行一个抽象。从工程的角度上来讲，这两个协议其实可以合并为一个单独的协议，因为这两个协议会被组合使用。

然而为了清楚起见，在本例中我们依然分开定义这两个协议：

1
2
3
4
5
(defprotocol Each
  (each [v op w]))

(defprotocol Distance
  (distance [v w]))

在Each协议中定义的each函数中，将一个操作行为op作用在两个序列v和w对应位置的元素上，也就是遍历v和w两个序列中每一个位置的值，将对应位置的两个元素传入op函数中得到一个新的结果。each函数和标准库中的map函数很类似，但是each函数可以根据序列w中元素的数据类型来决定如何使用函数op。Distance协议中定义的distance函数用来计算两个集合v和w表示的两个向量之间的距离值。注意到我们使用通用的描述”集合”因为我们现在看到的是一个抽象协议，而不是这些协议中函数的具体实现。我们将在本例中实现上面两个协议，并将实现的实例作为嵌入到clojure.lang.PersistentVector这个数据类型中。当然我们也可以将其他的数据类型也实现这个协议中的函数，从而来扩展数据类型，比如map类型以及set类型。

在本节的例子中，我们将实现单点联动聚类作为联动标准。首先我们要定义一个函数来从一个向量集合中确定两个距离值最小的向量。为了做到这一点，我们可以使用min-key函数，这个函数可以返回一个序列中最小值对应的键，即使这个序列是一个向量(vector)类型。有趣的是，在Clojure中的确是可行的，因为我们可以把一个vector类型的对象也当做是一个map类型的对象，其中每一个元素对应的下标值就可以看做是这个元素对应的键。我们用如下代码可以实现选择最近两个向量的函数：

1
2
3
4
5
6
7
(defn closest-vectors [vs]
  (let [index-range (range (count vs))]
    (apply min-key
           (fn [[x y]] (distance (vs x) (vs y)))
           (for [i index-range
                 j (filter #(not= i %) index-range)]
             [i j]))))

上面代码定义的closest-vectors函数使用for形式确定了序列vs中所有可能出现的两两下标组合。需要注意的是vs是一个内部元素也为向量类型的向量。然后根据得到的所有下标组合从vs中取出相应的一对向量然后传给distance函数来计算这一对向量之间的距离大小，然后用min-key函数来逐个比较所有计算出来的距离值。这个函数最后会返回距离值最最小的一对向量对应的下标值，进而来实现单点联动聚类。

我们还要计算每一次通过closest-vectors函数选出来的两个需要被组合为一个簇的向量的均值，我们可以利用之前在Each协议中定义的each函数以及Clojure中的reduce函数来做到这一点，如下所示：

1
2
3
4
5
(defn centroid [& xs]
  (each
   (reduce #(each %1 + %2) xs)
   *
   (double (/ 1 (count xs)))))

上面代码定义的centroid函数会计算一个向量序列中所有向量的平均值。需要注意的是要使用double函数来保证centroid函数返回的重心向量中每一个元素的数据类型是双精度浮点数。

我们现在来将Each协议和Distance协议扩展到Clojure中的向量数据类型，并且实现两个协议中制定的行为，使得这些行为成为clojure.lang.PersistentVector数据类型的一部分，达到了扩展语言自身的效果，我们可以使用extend-type函数来做到这一点，如下代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
(extend-type clojure.lang.PersistentVector
  Each
  (each [v op w]
    (vec
     (cond
      (number? w) (map op v (repeat w))
      (vector? w) (if (>= (count v) (count w))
                    (map op v (lazy-cat w (repeat 0)))
                    (map op (lazy-cat v (repeat 0)) w)))))
  Distance
  ;; 实现了欧氏距离计算行为
  (distance [v w] (-> (each v - w)
                      sum-of-squares
                      sqrt)))

上面代码中首先实现了each函数，从而可以将op操作作用在第一个参数v和第二个参数w上，其中参数v是一个向量类型的参数，参数w则既可以是数字也可以是向量类型。假如w是一个数字，那么我们先用repeat函数来构造一个所有元素都是w的无限长的惰性序列，然后利用map函数将op行为作用在向量v和这个惰性序列上，从而得到一个新的序列作为each函数的结果。假如w是向量类型，在这种情况下我们还要判断v和w两个向量的长度是否一致，如果不一致，我们需要用lazy-cat函数在较短的那个向量后面进行补零操作，这同样产生一个无限长的惰性序列，然后再用map函数将op行为作用到未进行补零操作的向量和经过补零操作之后的惰性序列上。需要注意的是，each函数内计算的结果要返回是需要经过vec函数的包装，从而保证返回的结果总是向量类型。

上面代码之后实现了distance函数，在这个函数中我们使用clojure.math.numeric-tower名字空间下的sqrt函数以及之前实现的sum-of-squares函数来计算传入的两个向量v和w之间的欧氏距离的值。

现在我们已经有了要实现一个可以对一组向量数据集进行层级聚类的函数的所有基础部分。我们可以用之前定义的centroid函数和closest-vectors函数来大致地实现一个可以用来层级聚类的函数，如下面代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(defn h-cluster
  "对于给定的数据集进行层级聚类，其中传入的数据集应该是一个
  每一个元素都是一个map对象且格式为{:vec [1 2 3]}的序列。"
  [nodes]
  (loop [nodes nodes]
    (if (< (count nodes) 2)
      nodes
      (let [vectors    (vec (map :vec nodes))
            [l r]      (closest-vectors vectors)
            node-range (range (count nodes))
            new-nodes  (vec
                        (for [i node-range
                              :when (and (not= i l)
                                         (not= i r))]
                          (nodes i)))]
        (recur (conj new-nodes
                     {:left (nodes l) :right (nodes r)
                      :vec (centroid
                            (:vec (nodes l))
                            (:vec (nodes r)))}))))))

我们可以将一组格式化的每一个元素都是map对象的向量传递给上面代码定义的h-cluster函数。在传入的向量中，每一个map对象中只有一个键值对，其中键为:vec而值则是一个描述样本点特征值的向量。h-cluster函数首先利用:vec关键字从所有map对象中提取出了输入样本点，并使用closest-vectors函数来确定两个距离最近的样本点。因为closest-vectors函数返回的值是一个含有两个距离最近样本点对应的下标值的向量，所以我们必须将除了由closest-vectors确定的两个向量以外剩下的向量重新组成一个新的待聚类向量集。我们可以使用for这个特殊的宏来做到这一点，在这个宏中我们可以使用:when关键字来指定一个判断用的条件从句。然后我们使用centroid函数来计算之前选出来的两个距离最近的向量的平均值作为新产生的簇的重心值。然后利用计算出来的重心值来生成一个新的map对象加入到之前生成的待聚类向量集中，而之前已经选出的两个距离最近的样本点将不会再出现在待聚类的向量集中了。然后使用loop形式让上述过程不断迭代，直到所有样本点都聚类到了一个簇中为止。我们可以在REPL中查看h-cluster函数的行为，如下面代码所示：

1
2
3
4
5
6
user> (h-cluster [{:vec [1 2 3]} {:vec [3 4 5]} {:vec [7 9 9]}])
[{:left {:vec [7 9 9]},
 :right {:left {:vec [1 2 3]},
         :right {:vec [3 4 5]},
         :vec [2.0 3.0 4.0]},
 :vec [4.5 6.0 6.5] }]

如上面代码所示，待聚类的样本集中的三个样本分别是[1 2 3]，[3 4 5]以及[7 9 9]，h-cluster函数先将[1 2 3]和[3 4 5]两个样本分组到了一个簇中，这个新产生的簇的重心值可以利用[1 2 3]和[3 4 5]两个向量来进行计算，结果为[2.0 3.0 4.0]。再进行第二次聚类迭代时，这个新产生的簇和[7 9 9]这个样本一起合并为了一个新的簇，而此时所有样本都被分组到了同一个簇中，聚类操作也结束了，最终得到的簇的重心值为[4.5 6.0 6.5]。因此我们可以看到，使用h-cluster函数可以用来将待聚类样本进行层级聚类将所有的样本都聚集到一个簇中，并且可以看到每一次聚类的结果以及整个聚类过程得到的层级结构，方便后续划分。需要注意的是，在上面的例子中为了实现的简便起见，我们在计算两个簇之间的距离时并没有严格按照单点联动聚类里规定的准则，而是直接用了两个簇的重心之间的距离来作为聚类的标准。

clj-ml库中提供了一种Cobweb层级聚类算法的实现，我们可以将:cobweb关键字传给make-clusterer函数从而得到一个Cobweb层级聚类器的实例，如下面代码所示：

1
(def h-clusterer (make-clusterer :cobweb)

上面代码中使用h-clusterer变量定义的聚类器可以使用之前定义过的train-clusterer函数和iris-dataset数据集来进行训练，如下面代码所示：

1
2
3
4
5
6
7
8
9
user> (train-clusterer h-clusterer iris-dataset)
#<Cobweb Number of merges: 0
Number of splits: 0
Number of clusters: 3

node 0 [150]
|   leaf 1 [96]
node 0 [150]
|   leaf 2 [54]

在如上所示REPL的输出中，Cobweb聚类算法将输入的待聚类数据集聚类到了两个簇中国。其中一个簇有96个样本，而另一个簇有54个样本。这个聚类结果与我们之前使用K-means算法进行聚类之后的聚类结果很不一样，在这个情况下Cobweb聚类算法的性能显然没有K-means聚类算法的性能好。总的来说，clj-ml库让我们很容易地就可以创建并且训练一个Cobweb聚类器。

使用期望极大(EM)算法

期望极大(EM)算法是一种利用概率估计的方法来确定一个聚类模型从而拟合给定的训练数据集。这个算法对定制的预估模型参数进行极大似然估计(MLE)，从而找到一组最佳的模型参数用于聚类操作(更多信息可以参考”Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable”这篇论文)。

假设我们在抛掷硬币的时候需要确定此时硬币正面朝上和反面朝上。假如我们抛掷次，抛掷完之后其中有次硬币正面朝上，有次硬币反面朝上。我们可以将硬币正面朝上的次数占总共抛掷硬币次数的比率作为近似估计的硬币正面朝上的概率，如下面等式所示：

上面等式中定义的似然概率就是硬币正面朝上真实概率的极大似然估计(MLE)。在机器学习领域中，极大似然估计可以被用来最大化某一个类别出现的概率。然而，大多数情况下对于给定的训练数据，估计出来的概率可能不会符合一个可以精确定义的统计分布，也使得很难有效的对训练数据中的概率分布进行极大似然估计，这是因为在训练数据中存在无法观测到的变量值，所以我们可以通过引入隐藏变量来表示数据集中无法观测到的值的方法来简化问题，这些隐藏变量的值无法直接从数据集中测量或者计算得到，但是可以通过假设再验证的方法或者从对影响训练数据的因素来确定。最终似然函数有三个参数，第一个是本身就需要利用极大似然估计来进行估计确定的概率分布参数，第二个参数是可以从数据集中观测到的值，第三个参数是数据集中的隐含值。这个极大似然函数也被定义为在给定一组概率分布参数的条件下，和出现的概率，为了能让真实存在的事实尽可能地发生，所以我们需要让这个极大似然函数的值尽可能的大。这个似然函数在数学上的表示为，可以用如下表达式来表述：

EM算法包含两个步骤-估计(E)步骤与最大化(M)步骤。在估计步骤中，我们计算以对数形式表示的似然函数的估计值，这一步骤中最终计算得到的结果可以表示成一个函数，而在下一个步骤，也就是最大化步骤中需要最大化这个函数的值。这两个步骤可以形式化地表述如下：

根据上面等式定义的EM算法步骤，我们需要不断迭代个更新步骤，每一步中都需要计算出一个新的参数，或者说是对数据集的一组新的假设，从而在每一步迭代中最大化估计函数的值，直到收敛到一个局部最优的值。这一项表示EM算法在第次迭代时计算得到的概率分布估计参数，此外这一项表示的是以对数形式表示的似然函数的期望值，也就是函数。

clj-ml库中同样提供了EM算法的实现，我们可以将:expectation-maximization关键字作为参数传给make-clusterer函数，从而创建一个EM聚类器，如下面代码所示：

1
2
(def em-clusterer (make-clusterer :expectation-maximization
                                  {:number-clusters 3}))

需要注意的是，如上面代码所示，我们还需要显式地指定最终聚类得到的簇的个数，并作为配置参数传给make-clusterer函数。

现在我们可以用之前定义过的train-clusterer函数和iris-dataset变量表示的数据集来训练上面代码中定义的用em-clusterer变量表示的EM聚类器，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
user> (train-clusterer em-clusterer iris-dataset)
#<EM 
EM
==

Number of clusters: 3


               Cluster
Attribute            0       1       2
                (0.41)  (0.25)  (0.33)
=======================================
Sepal.Length
  mean           5.9275  6.8085   5.006
  std. dev.      0.4817  0.5339  0.3489

Sepal.Width
  mean           2.7503  3.0709   3.428
  std. dev.      0.2956  0.2867  0.3753

Petal.Length
  mean           4.4057  5.7233   1.462
  std. dev.      0.5254  0.4991  0.1719

Petal.Width
  mean           1.4131  2.1055   0.246
  std. dev.      0.2627  0.2456  0.1043

从上面的输出结果中可以看到，EM聚类器将给定数据集划分为了三个簇，其中训练数据集中有的样本被分到了第一个簇，的样本被分到了第二个簇，而最后剩下的的样本被分到了第三个簇中。

使用自组织神经网络

正如我们在第四章中提到的，自组织神经网络可以用来对非监督机器学习问题进行建模，比如聚类问题(更多信息可以参考”Self-organizing Maps as Substitutes for K-Means Clustering”这篇论文)。快速回顾一下，一个自组织神经网络(SOM)是人工神经网络中的一种，用来将一个在高维特征空间中的样本输入向量映射到一个维度较低的输出空间中。而且这种映射基本保留了输入样本数据集中的模式以及拓扑关系。经过训练后的自组织神经网络中输出空间的神经元会对某一类输入样本产生较高的激活值。因此在对样本处于较高维度的特种空间中的数据集进行聚类时使用自组织神经网络是一种不错的解决方案。

Incanter库提供了一种简单而优雅的自组织网络实现，可以让我们相对容易的构建一个自组织神经网络。在后面的例子中会演示如何使用Incanter库提供的自组织神经网络实现，并会对Iris数据集中的样本进行聚类。

要将Incanter库引入Leiningen项目中，我们需要将相应的依赖加入到project.clj文件中：

[incanter “1.5.4”]

在下面的例子中要在代码中使用Incanter库中的函数，我们需要修改代码中的名字空间声明从而引入Incanter库中的名字空间，如下所示：

(ns my-namespace

  (:use [incanter core som stats charts datasets]))

我们首先利用Incanter库中的get-dataset，sel和to-matrix函数来定义训练数据集，如下面代码所示：

1
2
3
4
5
(def iris-features (to-matrix (sel (get-dataset :iris)
                                   :cols [:Sepal.Length
                                          :Sepal.Width
                                          :Petal.Length
                                          :Petal.Width])))

上面代码中定义的iris-features变量实际上是一个大小的矩阵来表示从Iris数据集中选出的150个样本，而每一个样本有4个维度的特征。然后我们就可以使用这个创建好的训练数据集以及incanter.som名字空间中的som-batch-train函数来创建并训练一个自组织神经网络，如下所示：

1
2
(def som (som-batch-train
          iris-features :cycles 10 :alpha 0.5 :beta 3))

上面代码定义的som变量实际上是一个有很多组键值对的map对象。在这个map对象中:dims键对应的值是一个向量，这个向量中的元素是用来描述自组织神经网络输出层的晶格解构的，这里指的晶格解构其实就是第四章中描述自组织神经网络的图片上方的那一层输出神经元。我们可以在REPL中查看这个向量的值，如下所示：

1
2
user> (:dims som)
[10.0 2.0]

因此我们可以说当前生成的自组织神经网络的输出层的晶格形状是一个的矩阵。:sets键对应的值比较有意思，这个值依然是一个map对象，这个map对象中的键表示最终聚类结束后自组织神经网络输出层激活值最高的三个神经元节点在晶格结构中的坐标位置，，也就是最终聚类后的簇的中心神经元节点，而map对象的值就是被分组到中心神经元节点对应的簇中所有样本点在原训练数据集中的下标值。我们同样在REPL中进行查看，如下所示：

1
2
3
4
user> (:sets som)
{[4 1] (144 143 141 ... 102 100),
 [8 1] (149 148 147 ... 50),
 [9 0] (49 48 47 46 ... 0)}

如上面REPL输出结果所示，输入数据集被聚类成了三个簇。我们可以利用incanter.stats名字空间中的mean函数来计算每一个簇的重心值，如下面代码所示：

1
2
3
4
(def feature-mean
  (map #(map mean (trans
                   (sel iris-features :rows ((:sets som) %))))
       (keys (:sets som))))

我们可以使用Incanter库中的xy-plot，add-lines以及view函数来实现一个函数将上面求得的几个簇的重心位置画出来，如下面代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
(defn plot-means []
  (let [x (range (ncol iris-features))
        cluster-name #(str "Cluster " %)]
    (-> (xy-plot x (nth feature-mean 0)
                 :x-label "Feature"
                 :y-label "Mean value of feature"
                 :legend true
                 :series-label (cluster-name 0))
        (add-lines x (nth feature-mean 1)
                   :series-label (cluster-name 1))
        (add-lines x (nth feature-mean 2)
                   :series-label (cluster-name 2))
        view)))

调用我们上面定义的plot-means函数，我们可以画出以下的折线图：

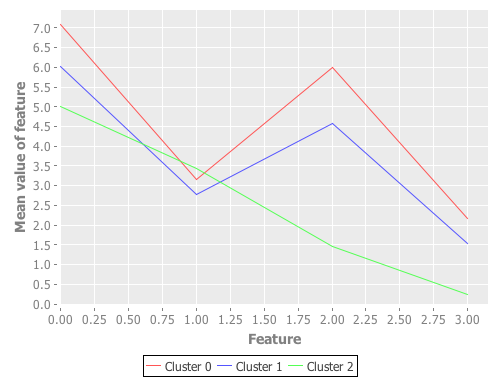
上面画出的折线图向我们展示了自组织神经网络(SOM)聚类之后每一个簇的重心值，其中上面每一条折线中每一个拐点对应的纵轴值就是每一个簇中每一个特征的平均值，也可以看到由于plot-means函数中实际上是将每个簇对应的重心序列的下标值作为横轴值，序列中的元素作为纵轴值，所以每一条折线都有四个拐点，对应的横轴值分别是0, 1, 2, 3。从上图中可以看到Cluster0和Cluster1这两个簇的重心位置很相近。然而，第三个簇Cluster2的重心位置则和其他两个簇的重心位置相差很大，因此这个簇对应的折线的形状也和其他两个簇对应的折线形状完全不一样。当然，上面的图并没有给我们更多关于输入样本数据围绕这些重心值(平均值)的分布情况或者是变化情况。因为现在每一个样本中都有四个特征，所以要画成图表观察只能是以上图所示的折线图的形式，为了更好地可视化这些特征值，我们需要将每一个样本数据中的特征维度变换到两个或者三个，这样就可以很好地可视化出数据集的特征空间。在本章中的后面一节中，将会详细讨论降低训练样本数据集中特征空间维度的概念与方法。

我们还可以利用sel函数与frequencies函数将聚类之后每一个簇中的样本的预测类别和真实类别打印出来，如下面代码所示：

1
2
3
4
5
6
(defn print-clusters []
  (doseq [[pos rws] (:sets som)]
    (println pos \:
             (frequencies
              (sel (get-dataset :iris)
                   :cols :Species :rows rws)))))

我们可以在REPL中调用上面代码定义的print-clusters函数，从而观察最终聚类的结果：

1
2
3
4
5
user> (print-clusters)
[4 1] : {virginica 23}
[8 1] : {virginica 27, versicolor 50}
[9 0] : {setosa 50}
nil

如上面的输出结果所示，virginica和setosa两个品种的花似乎可以被适当地划分到两个簇中。然而在含有versicolor品种样本的簇中也同样含有27个virginica品种的样本，要解决这个问题可以通过增大训练数据集中样本的数量或者为每一个样本添加更多的特征两种方法来进行补救。

总的来说，Incanter库为我们提供了一种非常简洁的自组织神经网络的实现，让我们可以很容易地利用给定的数据集来创建并且训练一个自组织神经网络聚类器，在上面的例子中我们将Iris数据集作为训练数据集。

使用降维技术

为了可以简单直观地可视化高维非标记样本数据集中样本点的分布情况，我们必须减小样本数据集的特征空间维度到两维或者三维。一旦我们将输入样本数据的特征维度降到两维或者三维，那么我们就可以较容易地以一种利于理解的方式将样本数据点可视化出来。这个减小输入样本数据特征维度的操作也被称为降维(dimensionality reduction)。因为这种技术可以减小样本数据的特征维度而又不会缺失一些重要的样本特征信息，所以这种技术也适用于数据压缩领域。

主成分分析(PCA)是降维技术中常见的一种，这种降维方法可以将输入样本中的所有特征变量变换为一组线性不相关的数量更少的特征变量(更多信息，可以参考”Principal Component Analysis”这篇论文)。而变换之后得到的那一组特征变量也成为样本数据的主成分(principal components)。

主成分分析将会使用一个协方差矩阵以及一种叫做奇异值分解(SVD)的矩阵操作来计算给定输入样本的主成分。协方差矩阵使用来表示，可以利用有个样本对应的输入向量组成的矩阵来确定这个协方差矩阵：

详细解释一下上面等式中的矩阵，假设样本集中每一个样本都有个特征，可以用向量形式表述每一个样本：

其中需要进行均值归一化，所以需要构造一个均值向量，如下所示：

根据协方差矩阵的定义：

我们可以根据上面构造的向量和协方差矩阵的定义来构造：

所以最终的协方差矩阵也可以构造出来，：

在计算协方差矩阵时需要将输入样本值进行均值归一化，要确保每一维特征的均值是0。此外在计算协方差矩阵之前，也可以对特征的值进行缩放。接下来，我们需要确定协方差矩阵的奇异值分解，如下所示：

奇异值分解可以看做是将大小为的矩阵因式分解为三个矩阵，和。其中矩阵的大小是，矩阵的大小为，矩阵的大小为。矩阵实际上表示了有个特征数量为的输入向量的样本数据集。矩阵是一个对角矩阵，也称为矩阵的奇异值(singular value)，而矩阵和矩阵分别为矩阵的左奇异值(left singular value)和右奇异值(right singular value)。在主成分分析中，矩阵也称为样本数据的削减因子(reduction component)，而矩阵称为样本数据的旋转因子(rotation component)，其实可以看到假如每一个样本有个特征，那么最终得到的协方差矩阵将会是阶的方阵。

主成分分析算法将个代表样本的输入向量的特征空间从维减小到维。这个降维的过程可以描述成一下的步骤：

  1. 利用输入矩阵(上文中已经详细描述了这个矩阵的构造过程)，来计算得到协方差矩阵。
  2. 利用奇异值分解将协方差矩阵因式分解为三个矩阵，以及。
  3. 从阶的矩阵中选出前列，选取的方法是画出奇异值矩阵中对角线上的奇异值分布，然后取较大的前K个奇异值对应的奇异值向量，也就是矩阵的前列(这和利用特征值分解进行主成分分析很类似)，得到一个新的矩阵，这个新的矩阵也称为协方差矩阵的左削减奇异值向量(reduced left singular vector)或者削减旋转矩阵(reduced rotation matrix)。这个矩阵表示了样本数据中前个主成分，所以这个矩阵的大小是阶。
  4. 计算原样本数据经过降维之后的输入矩阵，计算公式如下所示：

需要注意的是，最终出入给主成分分析算法进行降维的输入矩阵需要经过均值归一化以及特征值缩放操作也就是上面公式中的与我们构造协方差矩阵时的矩阵一致，当然上面公式中的矩阵也可以与上文中用来计算协方差矩阵时用到的矩阵不同，这里所指的矩阵仅仅是由所有输入样本向量组成的输入矩阵，而不需要进行均值归一化操作也不需要进行特征值缩放操作，如下所示：

因为是一个阶的矩阵，是一个阶的矩阵，其中的代表每一个样本中特征的个数，代表数据集中样本的个数，代表降维后选取出的主成分的个数。所以最终得到的降维矩阵是一个阶的矩阵，表示了个有个特征的样本。需要注意到的是，将样本的特征维度从降到之后，可能会导致样本数据中产生更高的损耗方差，也就是数据分布会更加离散化，因此在实际使用中我们需要选择合适的值，从而让降维带来的误差尽可能得低。

原始输入矩阵同样也可以使用降维矩阵和左削减奇异值向量来重现，计算公式如下所示：

Incanter这个库同样提供了可以供使用者进行主成分分析操作的函数。在后面的例子中我们将会使用主成分分析来对Iris数据集中的样本进行降维，从而可以更好地对这些样本点的分布进行可视化。

在下面的例子中为了使用Incanter库中的名字空间以及各个名字空间下的函数，我们需要修改代码文件中的名字空间声明，如下所示：

(ns my-namespace

  (:use [incanter core stats charts datasets]))

我们首先使用get-dataset，to-matrix和sel函数来定义训练数据集，如下面代码所示：

1
2
3
(def iris-matrix (to-matrix (get-dataset :iris)))
(def iris-features (sel iris-matrix :cols (range 4)))
(def iris-species (sel iris-matrix :cols 4))

和之前的例子类似，我们取Iris数据集的前四列作为样本输入值，而这些样本也构成了我们训练主成分分析算法寻找矩阵的训练数据集。

我们可以使用incanter.stats名字空间下的principal-components函数来执行主成分分析操作。这个函数会返回一个map对象，这个map对象中存储了上文中提到的主成分分析算法生成的削减矩阵与旋转矩阵。我们可以在REPL中查看这个map对象中的内容：

1
2
3
4
5
6
7
8
9
10
(def pca (principal-components iris-features))
user> pca
{:std-dev (1.7083611493276223 0.9560494084868574 0.383088600158391 0.1439264966176126),
 :rotation  A 4x4 matrix
  -------------
 -5.21e-01 -3.77e-01  7.20e-01  2.61e-01 
  2.69e-01 -9.23e-01 -2.44e-01 -1.24e-01 
 -5.80e-01 -2.45e-02 -1.42e-01 -8.01e-01 
 -5.65e-01 -6.69e-02 -6.34e-01  5.24e-01 
}

可以看到，:rotation键对应的值是旋转矩阵，:std-dev键对应的值是削减矩阵，只不过此时的矩阵并不是以矩阵形式存储，而是以序列形式存储矩阵中对角线上的非零值。

现在我们可以使用sel函数从输入数据的旋转矩阵中取前几列得到左削减奇异值向量，如下面代码所示：

1
2
(def U (:rotation pca))
(def U-reduced (sel U :cols (range 2)))

如上面代码所示，我们可以用:rotation关键字来从principal-components函数返回的map对象中获得用输入数据对主成分分析算法进行训练之后得到的旋转矩阵。现在我们可以利用削减旋转矩阵以及用iris-features变量表示的原输入样本矩阵来计算降维特征矩阵，如下面代码所示：

1
(def reduced-features (mmult iris-features U-reduced))

从上面计算降维特征矩阵的代码中可以看到，与我们之前定义的公式中的形式稍有不同，这是因为代码中得到的各个矩阵的阶次形状与上文理论部分讨论中定义的各个矩阵的阶次形状不同，其实两者是等价的，最终得到的计算结果也是一致的，读者可以自行体会。

在经过降维之后得到的数据样本矩阵中每一个样本的特征数就从原来的4维降到了2维。然后我们就可以使用scatter-plot函数将reduced-features函数返回的降维特征矩阵中的每一个样本点画出来，从而可以有效地对原数据集中样本点的分布情况进行可视化，如下面代码所示：

1
2
3
4
5
6
(defn plot-reduced-features []
  (view (scatter-plot (sel reduced-features :cols 0)
                      (sel reduced-features :cols 1)
                      :group-by iris-species
                      :x-label "PC1"
                      :y-label "PC2")))

调用上面代码定义的plot-reduced-features函数画出的样本分布情况如下图所示：

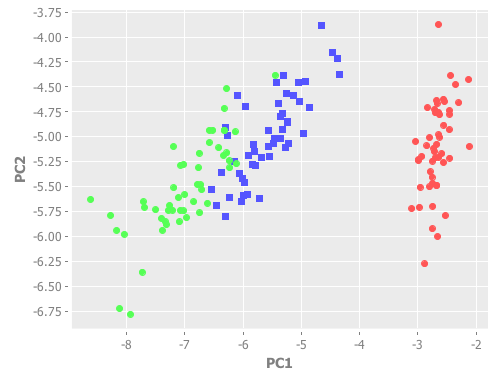
如上面所示的散点图很好地为我们可视化了原数据集中样本点的分布情况。和之前用折线图画出的聚类簇均值图类似，从上图中可以看到有两类数据样本在给定的特征空间中比较相似，样本点靠得很近，而另一类样本点则可以很好地与其他两类样本进行区分，因为在给定的特征空间中，这一类样本点分布的位置较为孤立。综上所示，Incanter库可以很好地支持主成分分析操作，从而可以有效的让我们降低高维数据样本的特征维度从而可以比较直观和容易地可视化样本点的分布情况。

本章概要

在这一章中，我们探索了几个可以对非标记数据集进行建模的聚类算法。本章的要点可以概括如下：

  • 使用纯Clojure实现了K-means聚类算法以及层级聚类算法，并且分别用训练数据训练了这两个实现的聚类模型，较为深入的理解了两种聚类算法。此外还介绍了如何使用clj-ml库来更为简单地使用这两种聚类算法。
  • 讨论了期望极大(EM)算法，这种算法是一种基于概率统计理论的聚类算法。在讨论完EM算法的理论之后，使用clj-ml库创建并训练了一个EM聚类器。
  • 此外还探索了使用自组织神经网络(SOM)来拟合在高维特征空间中的聚类问题。介绍了使用Incanter库来创建并训练一个自组织神经网络并用这个训练好的实例来进行聚类操作。
  • 最后，学习了降维技术的概念与主成分分析算法，以及如何使用主成分分析技术来对Incanter库中的Iris数据集中的样本数据进行特征降维，从而可以更好地可视化这个数据集中样本点的分布情况。

在下一章中，我们将会探索异常检测的概念以及利用机器学习的技术来构建推荐系统。