cljmlchapter4-ann

,

在这一章中，我们将会介绍人工神经网络(ANNs)。我们将会学习ANNs的基本知识和概念并且对可以解决监督学习和非监督学习的几个ANN模型进行讨论，最后会介绍Enclog这个clojure的库去构建ANNS。

神经网络非常适合于从给定的数据集中寻找一种特定的模式，并且有许多实际应用，比如说手写字识别和计算机视觉。ANNs通常通常是以一种融合的方式去对给定的问题进行建模寻找模式。有意思的是，神经网络可以被应用在多种机器学习问题上，比如回归和分类问题。ANNs在计算机科学的其他领域都有广泛的应用，而不单单是局限在机器学习的研究上。

非监督学习是机器学习中的一种形式，此类问题中给定的训练数据集中并没有标注训练样本的输出是属于哪一个类别。由于训练数据集是非标注的，所以一个非监督学习算法必须完全靠它自己去确定每一个样本的输出所对应的类别。通常情况下，非监督学习算法会寻找训练样本之间的相似性，然后将它们分组归类到几个不同的类别中。这样的技术通常也叫聚类分析，在后面的章节中我们会更深入的学习这种方法论。ANNs被用在非监督学习领域更多的是得益于其在非标注数据集中能快速发现特征的能力。这中由ANNs表现出来的非监督学习的特殊形式也成为竞争学习。

关于人工神经网络的一个有趣的事实是，它们是由高等生物中表现出学习能力的中枢神经系统的结构和行为建模得到的。

理解非线性回归

目前为止，读着必须知道的一个事实就是在使用线性回归和逻辑斯蒂回归解决回归和分类问题时可以使用梯度下降算法来估计参数。随之而来的一个问题就是，既然我们已经可以使用梯度下降算法和训练数据来估计调整线性回归和逻辑斯蒂回归模型的参数，那我们为什么还需要神经网络。要理解为什么需要神经网络，我们首先需要理解非线性回归。

让我们假设现在有一个单特征变量X和一个因变量Y，Y随着X的变化曲线如下图所示

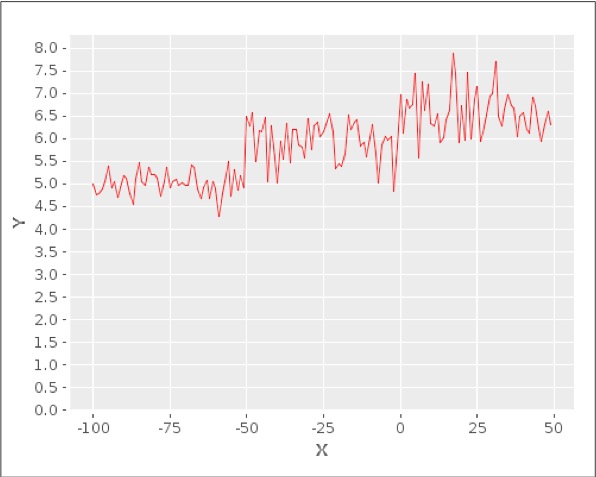
如上图所示，使用线性等式非常难甚至是不可能对因变量Y和自变量X之间的关系进行建模。我们只能用高阶多项式才能对Y和X之间的关系进行建模，从而将问题转化为线性回归的标准形式。因此因变量Y和自变量X之间的关系是非线性的，在Y和X的关系式中存在X的高阶项。当然，也很有可能连高阶多项式都没有办法建模去拟合Y和X之间复杂的非线性关系。

可以看到使用梯度下降算法去更新一个多项式函数中的所有权重或者系数的值带来的时间复杂度是，其中n是训练数据集中的特征个数。计算一个三阶多项式所有项的系数的算法复杂度是。可以看到梯度下降算法的时间复杂度随着模型中的特征数的增多以几何级增长。因此梯度下降算法在对拥有大量特征非线性回归问题建模时非常的低效。

而ANNs，在对拥有高维度特征的数据集进行非线性回归建模时十分高效。我们将会学习ANNs中的一些基础概念以及几个可以应用在监督学习和非监督学习问题上的ANN模型。

描述神经网络

ANNs是根据生物体，比如哺乳动物和爬行动物中拥有学习能力的中枢神经系统的行为来进行建模的。这些生物体的中枢神经系统包括生物体的大脑，脊髓和支持神经组织的网络。大脑处理信息并且产生电信号，并将这些电信号通过神经纤维组成的网络传输到生物体中不同的器官上。尽管生物体的大脑需要进行非常复杂的计算和控制任务，但是它实际上只是神经元的一个集合。对应生物体感官信号的处理实际上也是由这些神经元组成的多个复杂的网络来进行的。当然，每个神经元只能处理由大脑处理的信息中的非常小的一部分。大脑的功能其实是将不同感知器官产生的电信号通过由神经元组成的复杂网络路由到运动器官上。一个独立的神经元有如下图所示的细胞结构。

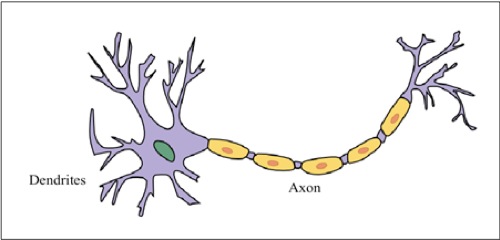
一个神经元有有多个靠近细胞核的树突和一个用来传递神经元细胞核信号的轴突。树突通常是被用来接受从其他神经元中发出的信号，并且将这些接收到得信号作为当前神经元的输入信号。类似的，神经元的轴突就相当于是神经元的输出。因此一个神经元可以被数学化地描述成为一个接收多个参数作为输入并且有一个输出的函数。

神经元之间通常都是相互连接的，这些神经元连接起来形成的网络就被称为神经网络。一个神经元本质上就是接收微弱的电信号，然后再将电信号传递给其他的神经元。两个神经元之间相互连接的空间也叫做突触。

ANN由多个相互连接的神经元连接组成。每一个神经元都可以被抽象成一个具有多个输入和单个输出的数学函数，如下图所示：

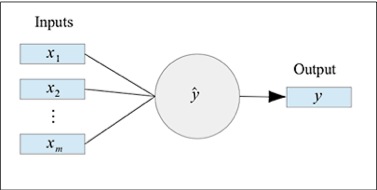
单个的神经元可以被上面的图像所描述。从数学的角度上来说，只是一个简单的函数，这个函数将多个输入值映射到一个输出，函数就被称为是激活函数。神经元在这种表示情况下也被称作感知器。感知器可以被单独使用，并且足以对一些监督学习模型比如线性回归和逻辑斯蒂回归进行模拟和评估。当然，复杂的非线性数据最好还是使用多个相互连接的感知器来进行建模。

通常情况下，有一个常数值会作为偏差项作为感知器的一维输入，对于输入，我们添加一个作为偏差输入，我们另。一个加上了偏差输入的神经元可以被表示成下图所示的样子：

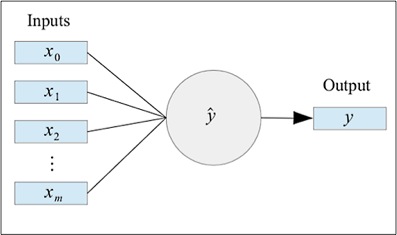
对于感知器的每一个输入，都有一个对应的权值。这个权值和线性回归模型中每一个特征对应的系数很类似。因此激活函数就是一个关于输入值及其对应的权值的一个函数。我们可以形式化通过输入，权值以及感知器的激活函数来定义感知器这个预计输出，如下面的公式所示：

其中

为激活函数

一个ANN节点所使用的激活函数很大程度上取决于待建模的训练数据。通常来说，sigmoid或者双曲正切函数会在分类问题上被用于作为激活函数(更多内容可以参考论文Wavelet Neural Network (WNN) approach for calibration model building based on gasoline near infrared (NIR) spectr)。sigmoid函数是否激活取决于输入是否能达到阈值。我们可以画出sigmoid函数的变化曲线来描述这种行为，如下图所示：

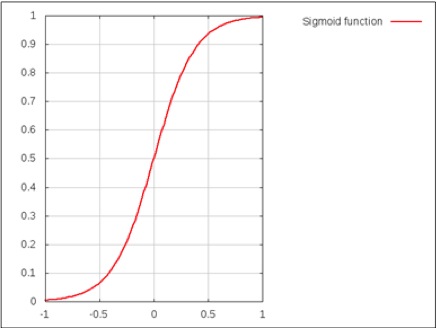
ANNs可以大致被分为前馈神经网络和递归神经网络(更多内容可以参考论文Bidirectional recurrent neural networks)。这两种神经网络的区别在于，前馈神经网络不会形成一个有向循环，而递归神经网络则会通过节点之间的连接形成一个有向环。因此前馈神经网络每一个节点只能从节点所在层的上一层接受输入。有许多神经网络模型都有实际的应用，我们将会在接下来的章节中对其中的一些进行探讨。

理解多层感知器神经网络

现在我们来了解一种简单的前馈神经网络模型-多层感知器模型。这个模型展示了前馈神经网络基本的样子并且在监督学习领域去对回归和分类问题进行建模拥有足够的通用性。在前馈神经网络中所有的输入都是单向流动的。这也是为什么在前馈神经网络中的任意一个层级上都没有反馈存在。
这里的反馈指的是在神经网络中的某一个给定层的输出又会作为输入反向作用在先前层级的感知器上。使用单层的感知器意味着只有一个激活函数，从而和使用逻辑斯蒂回归去对给定的训练数据进行建模有着相同的效果。这意味着这个模型无法去对非线性数据进行建模，而这也正是我们为什么需要ANNs。一定要注意，我们在第三章，对数据分类中已经讨论过了逻辑斯蒂回归。

一个多层感知器人工神经网络可以用下图来直观的描述：

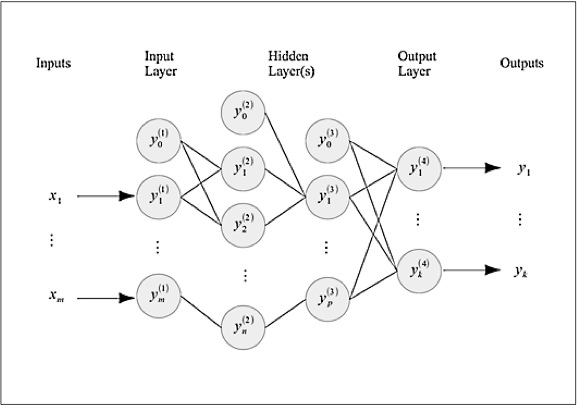
一个多层感知器神经网络是由许多层感知器节点组成的。如上图所示，有一个输入层，有一个输出层和若干隐含层，而每一层中又是由若干感知器组成的。输出层接收输入值，然后利用每个输入对应的权值以及激活函数计算出新的输出，并将这些新的值传递给下一个隐含层。

训练数据集中的每一个样本都可以被表示成，其中表示的第i个样本的期望输出，表示的是第i个样本的输入。其实是一个长度为训练数据中特征数量列向量。

每一个感知器节点的输出都可以被称为是这个节点的激活值，第l层第i个节点的激活值就被表示成为。正如之前提到的用于计算激活值的激活函数通常选用sigmoid函数或者双曲正切函数。当然任何其他的数学函数都可以作为激活函数去拟合特定的训练数据。多层感知器网络的输入层加上了一个偏移量到输入向量中，作为神经网络的最终输入，并且后面一层的输入值就是之前一层的激活值。可以用下面的等式表示这种关系：

神经网络的每一对前后图层之间都有一个相对应的权重矩阵。这些权重矩阵的列数和靠近输入层的层级中节点的个数相同，行数和靠近输出层的层级中节点的个数相同，对于第l层来说，权重矩阵可以被表示成：

神经网络第l层的激活值也可以使用激活函数计算出来。将权值矩阵和上一层的激活值向量相乘得到的结果作为传入激活函数。通常情况下，在多层感知器模型中使用sigmoid函数作为激活函数。上面的过程可以使用下面的公式来表示：

其中

是激活函数。

通常情况下，多层感知器神经网络使用sigmoid函数作为激活函数。需要注意的是我们没有在输出层增加一个偏移量。同样的，输出层可以产生任意的输出值。为了对一个k分类分类问题进行建模，神经网络需要产生k个输出值。

对于二分类问题，我们仅仅需要对一个至多只有两个类别的输入数据进行建模。ANN产生的输出不是0就是1。因此对于k=2的分类问题，。

同样地对于多分类问题，可以使用k个二分类的输出去模拟，所以输出值是一个的矩阵，如下所示：

至此，我们可以使用多层感知器神经网络去解决二分类和多分类问题。在后面的章节中我们将会学习并且实现反向传播算法来训练多层感知器神经网络。

架设我们现在要多异或门的行为进行建模。异或门可以被想象成是一个具有两个输入和一个输出的而分类器。如下图所示是一个对异或门进行建模的神经网络的结构。有趣的是，线性回归可以被用于对与门和或门进行建模但是却没有办法对异或门进行建模。这是因为异或门的输出是非线性性质的，而神经网络却可以很有效的解决这个问题。

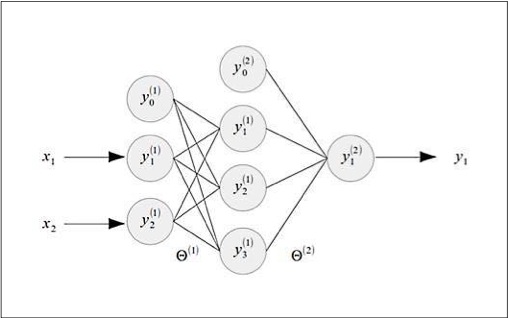
上图显示的多层感知器的输入层有三个节点，隐含层有四个节点，输入层有一个节点。可以看到除了输出层，每一层都加上了一个偏移输入。这个神经网络有两个突触，并且对应的有两个权值矩阵和，注意到第一个突触是在输入层和隐含层之间，第二个突触是在隐含层和输出层之间。所以权值矩阵是一个的矩阵，而权值矩阵是一个的矩阵。也通常被用来表示神经网络中的所有权值。

既然已经使用sigmoid函数作为多层感知器神经网络每个节点的激活函数，我们可以参照逻辑斯蒂回归模型类似的定义一个关于每一个节点权值的损失函数。神经网络的损失函数可以被定义成是以权值矩阵为变量的函数，如下所示：

上面所示的损失函数本质上是神经网络输出层上每一个节点的损失函数的平均值(更多细节参考论文Neural Networks in Materials Science)。对于一个有个输出的多层感知器神经网络来说，我们多这个因子的求平均。需要注意的是表示神经网络的第个输出，表示神经网络的输入，表示训练数据集中样本的数量。这个损失函数本质上是在量化一个有个输出的逻辑斯蒂回归。我们可以给之前的损失函数增加一个正则化系数来表示一个正则化损失函数，如下所示：

上面加上了正则化因子的损失函数和逻辑斯蒂回归中的正则化损失函数也非常的类似。正则化因子本质上是神经网络中所有权值的平方和，但是不包括偏移输入的权值。表示的是神经网络中第层的节点的个数。有趣的是在上面的正则化损失函数中，只有正则化因子是依赖于神经网络的层数的。因此一个神经网络预估模型的泛化能力是基于这个神经网络的层数的。

理解反向传播算法

反向传播学习算法利用给定的训练集来对多层感知器神经网络进行训练。简单的来说，这个算法首先利用给定的输入值来计算输出值，然后计算神经网络的输出误差量。神经网络的输出误差量是对比真实输出和训练数据集中的期望输出来计算得到的。再利用计算出来的误差来更新神经网络的权值。因此当用一定量的样本对神经网络训练完之后，这个神经网络将有能力为给定的输入预测出输出值。这个算法包含独立的三个步骤，如下所示：

  • 前向传播阶段
  • 后向传播阶段
  • 更新权值阶段

神经网络突触上的权值矩阵中的每一个元素首先初始化成一个小范围内接近零的随机数，这个范围表示为。在这个范围内随机地初始化权值是为了避免权值矩阵出现对称的情况，为了避免对称采取的行为叫做对成型破缺，这是为了让神经网络的突触上的每一个权值在每一次用反向传播算法进行迭代的时候能够产生明显的改变。这也描述了在神经网络中每一感知器节点都是相互独立地进行学习。假如所有节点都有相同的权值，那么训练学习出来的预估模型就很有可能是欠拟合的活着是过拟合的。

此外，反向传播学习算法还需要两个额外的参数，一个是学习速率，另一个是学习动量，在后面章节的例子中我们将会看到这两个参数的作用。

前向传播阶段只是简单的计算了神经网络每一层中所有节点的激活值。正如之前提到的神经网络输入层节点的激活值就是神经网络的输入值和输入偏移量，可以被形式化地定义为下面这个等式：

利用神经网络输入层的激活值，其他层节点的激活值也就随之确定了。这个过程是利用前一层的激活值和权值的乘积和传入激活函数，然后计算出当前层的激活值，可以使用下面的公式：

从上面的公式中可以看到第层的激活值是由前一层的激活值以及对应的权值的乘积作为激活函数的参数计算得到的。之后输出层的激活值就会被反向传播了，意思是，神经网络这些激活值将会通过隐含层从输出层反向传播到输入层。在这一个步骤中，我们需要计算神经网络每一个节点的误差量。输出层的误差值是利用期望的输出值和输出层的激活值的差值计算出来的，可以用下面的等式表示：

神经网络中除了输出层的其他层的误差项使用下面的公式计算：

在上面的等式中，这个符号用来代表相同形状的矩阵逐元素乘法的操作行文，需要注意的是这和矩阵相乘的操作不同，逐元素乘法会返回一个矩阵，这个矩阵中每一个元素都是由相乘的两个形状相同的矩阵对应位置的元素相乘得到的，所以做乘法的两个矩阵和计算得到的矩阵都有相同的形状，可以用下面的等式描述这种操作：

而这一项则表示的是神经网络中使用的激活函数的导，由于我们现在使用的是sigmoid函数，所以其实就是。

因此，我们现在可以计算神经网络中所有节点的误差值了。我们可以利用这些误差值去确定神经网络突触上的梯度。我们现在进入反向传播算法最后更新权值的这一步骤。
各个突触的梯度矩阵最初的时候都是使用去作为所有元素的初始值。突触的梯度矩阵和其对应的权值矩阵具有相同的形状。被用来表示神经网络中第层之后的突触的梯度矩阵，神经网络突触梯度矩阵的初始值通常为如下所示的形式：

对于训练数据集中的每一个样本，我们都会计算神经网络中每一个节点的误差和激活值。这些值会被加到突触的梯度矩阵中，如下所示：

然后计算矩阵矩阵的平均值，就是除以样本集的大小。然后利用误差矩阵和梯度矩阵去更新每一层的权值矩阵，如下面的表达式所示：

因此，反向传播算法中的学习速率和学习动量这两个参数只是在更新权重这个步骤中用到了。注意上面那个公式中的并不是指当前层的误差矩阵，而是当前层之前一次训练得到的权值变化量矩阵，动量项的意义也就在于要在上一次的权值变化方向上保持一定的惯性。之前提到的这三个公式就是反向传播算法中单次迭代的所有步骤了，需要进行大量的迭代更新操作直到神经网络的总误差收敛到一个很小的值。现在我们可以总结一下反向传播学习算法的所有步骤了：

  1. 使用很小范围内的随机数初始化神经网络突触的全职矩阵。
  2. 选取一个样本并且使用前向传播方法计算出神经网络中每一个感知器节点的激活值。
  3. 从输出层到输入层通过隐含层反向传播最后的输出层的激活值，这一步中，将需要计算神经网络每一个节点的误差
  4. 利用第三步计算得到的误差矩阵和突触的输入激活矩阵相乘得到神经网络中每一个节点的权重的梯度，每一个梯度都被表示成比率或者是百分比。
  5. 利用梯度矩阵和误差矩阵计算神经网络中每一个突触权重矩阵的变化量，然后对于的权重矩阵再去减去这个变化量，这就是反向传播算法更新权值的核心步骤了。
  6. 对剩下的样本数据重复步骤2至步骤5。

反向传播学习算法有许多独立的部分，我们会分别实现它们，并最终组成一个完整的算法实现。因为神经网络中突触的误差和权值以及激活值都可以被表现为矩阵形式，所以我们可以使用矩阵操作实现这个算法。

注意接下来的例子中，我们需要Incanter库中incanter.core这个名字空间里的函数。事实上在这个名字空间中的函数使用的是Clatrix这个库来表示矩阵和封装矩阵操作。

让我们架设我们现在需要实现使用神经网络去对异或门的逻辑行为进行建模。训练数据就只是简单的异或门的真值表，并且如下所示表示成向量的形式：

1
2
3
4
5
;;定义训练数据集
(def sample-data [[[0 0] [0]]
                  [[0 1] [1]]
                  [[1 0] [1]]
                  [[1 1] [0]]])

上面定义的向量sample-data中的每一个元素本身又是由异或门的输入向量和输出向量组成的。我们会利用这个向量形式的训练数据集来训练构建我们的神经网络模型。预测与非门的输出本质上是一个分类问题，我们将会使用神经网络对这个问题进行建模。从抽象意义上来说，一个神经网络需要具备解决二分类和多分类问题的能力，所以我们现在定义一个神经网络的抽象结构，如下面代码所示：

1
2
3
4
(defprotocol NeuralNetwork
  (run        [network inputs])
  (run-binary [network inputs])
  (train-ann  [network samples]))

上面代码定义的NeuralNetwork协议中有三个函数。train-ann函数被用来训练神经网络，并且需要一些训练样本数据。run和run-binary函数可以被用来解决多分类和二分类问题，两个函数都需要输入值。

反向传播算法的第一步是初始化神经网络每个突触对应的权值矩阵。我们可以使用rand和matrix函数去产生这些权值矩阵，如下面代码所示：

1
2
3
4
5
(defn rand-list
  "创建一个随机的双精度浮点数列表，其中每一个元素的取值范围在[-epsilon, epsilon]内。"
  [len epsilon]
  (map (fn [x] (- (rand (* 2 epsilon)) epsilon))
       (range 0 len)))
1
2
3
4
5
6
7
(defn random-initial-weights
  "对于给定的层级产生一个初识随机权值矩阵，layers参数中必须是由层级中节点数组成的一个向量。"
  [layers epsilon]
  (for [i (range 0 (dec (length layers)))]
    (let [cols (inc (get layers i))     ; 列的个数是输入的个数+1，因为要算上偏移量输入
          rows (get layers (inc i))]    ; 行的个数是下一层感知器节点的个数
      (matrix (rand-list (* rows cols) epsilon) cols))))

上面代码所示的rand-list函数创建了一个随机列表，其中的每一个元素的取值范围都在之间。如之前解释过的，我们需要以此来破坏权值矩阵的对称性。

random-initial-weights函数会为神经网络不同突触产生对应的权值矩阵。如上面代码定义的那样，layers参数必须是一个由神经网络各个层级中节点数量组成的向量。假如一个神经网络在输入层有两个节点，隐含层有三个节点，输出层有一个节点，就需要把[2 3 1]当做layers参数传给random-initial-weights函数。每一个权值矩阵的列数都和输入的个数相同，行数和下一层节点的个数相同，这里在输入中加上了一个额外的偏移量输入。需要注意的是我们使用了matrix函数的另一种形式，这种形式的第一个参数是一个向量，第二个参数是一个数值，目标输出的矩阵的列数是由第二个参数确定的，然后去将第一个参数表示的向量划分成一个矩阵。因此，作为第一个参数传入的向量必须有(* rows cols)个元素，其中rows和cols分别是权值矩阵的行数和列数。

因为对神经网络中的每一个节点我们都需要用sigmoid函数去计算激活值，所以我们必须定义一个函数，去对传入给定的输出矩阵中的每一个元素使用sigmoid函数得到激活值矩阵。我们可以使用incanter.core名字空间里的div，plus，exp和minus函数去实现这个功能，如下面的代码所示：

1
2
3
4
(defn sigmoid
  "对于传入的矩阵z，将其作为1/(1+exp(-z))函数的参数得到一个新的矩阵。"
  [z]
  (div 1 (plus 1 (exp (minus z)))))

注意之前定义过的所有函数中包含的算数运算都是作用在给定矩阵的所有元素上的，并且返回一个新的矩阵。

我们还必须隐式地向神经网络中得各层增加一个偏移量。可以通过实现一个bind-rows函数来封装这个操作，这个函数会对给定的矩阵增加一行元素，如下面的代码所示：

1
2
3
4
(defn bind-bias
  "在传入的向量上增加一个偏移量输入。"
  [v]
  (bind-rows [1] v))

因为偏移量的数值一般都是，所以我们在bind-bias函数中指定添加上的行元素为[1]。

使用之前定义的函数，我们就可以实现前向传播过程了。这个过程本质上是将神经网络两个层级之间的突出的权值和前一个层级产生的激活值相乘然后传入sigmoid函数中得到下一个层级的激活值，如下面的代码所示：

1
2
3
4
5
6
7
(defn matrix-mult
  "将传入的两个元素相乘，其中可能有元素是矩阵，并且保证函数返回的结果也一定是一个矩阵"
  [a b]
  (let [result (mmult a b)]
    (if (matrix? result)
      result
      (matrix [result]))))
1
2
3
4
(defn forward-propagate-layer
  "利用第l层和第l+1层之间突触对应的权值矩阵以及第l层的激活值矩阵计算第l+1层的激活值矩阵。"
  [weights activations]
  (sigmoid (matrix-mult weights activations)))
1
2
3
4
5
(defn forward-propagate
  "通过神经网络的权值矩阵前向传播激活值矩阵，并且将最终输出层的激活值返回。"
  [weights input-activations]
  (reduce #(forward-propagate-layer %2 (bind-bias %1))
          input-activations weights))

在上面的代码中，我们先定义了一个matrix-mult函数，这个函数可以将连个矩阵相乘，并且保证返回的也是一个矩阵。注意在matrix-mult函数中我们使用mmult而不是mult函数，因为mult函数是对两个相同形状的矩阵做逐元素乘法。

使用matrix-mult函数和sigmoid函数，我们可以实现神经网络中两个层级之间的前向传播步骤。这个步骤最终是在forward-propagate-layer函数中实现的，在这个函数中仅仅是将神经网络中两个层之间的突出对应的权值矩阵和输入的激活值矩阵相乘并且保证返回的一定是一个矩阵。在利用一组输入值在神经网络的所有层级之间前向传播的过程中我们必须在使用forward-propagate-layer函数为每一个层级增加一个偏移量输入，在上面代码定义的forward-propagate函数中就是用了将forward-propagate-layer函数放在reduce函数的闭包中来优雅的实现这个功能。

尽管forward-propagate函数可以确定神经网络的输出层激活值，但是我们仍然需要神经网络中其他节点的激活值来进行方向传播步骤。我们可以将reduce操作变成另一种递归操作，并且申明一个容器变量来存储神经网络中每一层的激活值矩阵。下面代码中定义的forward-propagate-all-activations函数就利用一个loop形式去递归的调用forward-propagate-layer函数从而实现获得每一个层级激活值矩阵的想法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(defn forward-propagate-all-activations
  "在神经网络中前向传播激活值矩阵，并且返回所有节点的激活值。"
  [weights input-activations]
  (loop [all-weights     weights
         ;;列向量上再加上一行
         activations     (bind-bias input-activations)
         all-activations [activations]]
    (let [[weights
           & all-weights'] all-weights
           last-iter?       (empty? all-weights')
           out-activations  (forward-propagate-layer
                             weights activations)
           activations'     (if last-iter? out-activations
                                (bind-bias out-activations))
           all-activations' (conj all-activations activations')]
      (if last-iter? all-activations'
          (recur all-weights' activations' all-activations')))))

上面代码定义的forward-propagate-all-activations函数需要神经网络所有节点的权值，并且将输入值当做初识激活值传入此函数。我们首先用了bind-bias函数在神经网络输入矩阵上加入了偏移量输入。然后我们用一个叫all-activations的容器去存放每一次产生的激活值矩阵，这个容器实际上时一个向量。然后forward-propagate-layer函数会作用在神经网络每一层的权值矩阵上，并且每一次迭代时都会在相关层级的输入上加上一个偏移量输入。

注意我们不会在最后一次迭代也就是计算到神经网络输出层的时候加上偏移量输入。因此forward-propagate-all-activations
函数会在前向传播过程中作用在神经网络每一层的节点上并且得到相应的激活值。要注意的是在all-activations这个向量中激活值矩阵的顺序是和神经网络中层级的顺序一致的。

现在我们来实现反向传播学习算法的反向传播步骤。首先我们需要实现利用公式来计算误差项的函数，如下面代码所示：

1
2
3
4
5
(defn back-propagate-layer
  "将第l+1层的误差反向传播计算并返回第l层的误差。"
  [deltas weights layer-activations]
  (mult (matrix-mult (trans weights) deltas)
        (mult layer-activations (minus 1 layer-activations))))

上面代码定义的back-propagate-layer函数利用神经网络第l层和第l+1层之间突触对应的权值矩阵以及第l+1层的误差来计算第l层的误差。

注意到我们仅仅是在用matrix-mult函数计算这一项的时候用到了矩阵乘法操作，另外其他的相乘操作都是利用mult函数进行的矩阵间逐元素相乘操作。

本质上来说，我们需要将上面的函数从输出层通过隐含层作用至输入层从而计算神经网络中每一个节点的误差值。这些误差值再作用到节点的激活之上，以此来产生来更新神经网络节点权值的梯度值。我们可以用一个和forward-propagate-all-activations函数类似的函数去递归将back-propagate-layer函数作用在神经网络的不同层上，以此来实现权值更新的行为。当然我们必须逆向地穿过神经网络的各个层级，也就是说从输出层开始，通过隐含层直到输入层，我们用下面的代码来实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
(defn calc-deltas
  "利用反向传播计算并返回神经网络中的所有误差包括输出层的误差。"
  [weights activations output-deltas]
  (let [hidden-weights     (reverse (rest weights))
        hidden-activations (rest (reverse (rest activations)))]
    (loop [deltas          output-deltas
           all-weights     hidden-weights
           all-activations hidden-activations
           all-deltas      (list output-deltas)]
      (if (empty? all-weights) all-deltas
        (let [[weights
               & all-weights']      all-weights
               [activations
                & all-activations'] all-activations
              deltas'        (back-propagate-layer
                               deltas weights activations)
              all-deltas'    (cons (rest deltas')
                                   all-deltas)]
          (recur deltas' all-weights' all-activations' all-deltas'))))))

calc-deltas函数确定了神经网络中每一个感知器节点的误差。在这个计算过程中并不需要输入层和输出层的激活值。我们仅仅需要隐含层的激活值去计算误差值，并将激活值绑定在hidden-activations变量上。同样的我们也不需要输入层对应的权值，然后将去掉输入层权值的权值矩阵绑定在hidden-weights变量上。然后calc-deltas函数就会用back-propagate-layer函数作用在神经网络每一个突触上的权值矩阵上，然后就可以以矩阵的形式得到所有节点的误差值了。需要注意的是我们没有将偏移量节点的误差加入到最终的结果集中，我们使用rest函数，(rest deltas')，作用在给定突触层的误差结果集上，因为结果集中的第一个误差是偏移量输入的误差，而当前层的偏移量与前一层是独立的，所以其误差也不需要向前一层反向传播。

根据之前的定义，突触层梯度向量这个因子是根据矩阵和相乘计算得到的，表示后面一层的误差矩阵表示当前给顶层级的激活值矩阵。我们可以用下面的代码实现计算梯度的过程：

1
2
3
4
(defn calc-gradients
  "利用误差和激活值计算梯度值。"
  [deltas activations]
  (map #(mmult %1 (trans %2)) deltas activations))

上面代码所示的calc-gradients函数优雅的实现了计算这一项。由于需要操作误差和激活值序列，我们使用map函数作用在之前等式所描述的神经网络中的误差矩阵和激活值矩阵。使用calc-deltas和calc-gradient函数，我们可以计算一个给定的训练样本在通过神经网络训练后隐含层每一个节点的误差以及对应层前一层的权重的梯度值，并且最终我们需要把这一次训练的输出误差平方和返回。可以使用下面的代码实现上述的过程：

1
2
3
4
5
6
7
8
9
10
11
12
(defn calc-error
  "对于给定的权值矩阵计算误差矩阵和平方误差项。"
  [weights [input expected-output]]
  (let [activations    (forward-propagate-all-activations
                         weights (matrix input))
        output         (last activations)
        output-deltas  (minus output expected-output)
        all-deltas     (calc-deltas
                         weights activations output-deltas)
        gradients      (calc-gradients all-deltas activations)]
    (list gradients
          (sum (pow output-deltas 2)))))

上面代码所定义的calc-error函数需要两个参数-神经网络突触对应的权值矩阵以及训练样本值，其中训练样本传入函数时会被解构成[input expected]的形式。首先会利用forward-propagation-all-activations函数来计算神经网络中所有节点的激活值，然后利用样本中的期望输出值和神经网络的实际输出值之间做差来计算输出层的误差值。神经网络计算出来的输出值，实际上就是利用forward-propagate-all-activations函数计算出来的激活值列表的最后一个元素，在上面的代码表示成(last activations)。使用计算出来的激活值矩阵和calc-deltas函数，就可以确定每一个感知器节点的误差值了。然后这些计算出来的误差值再被传入calc-gradients函数就可以用来确定神经网络前面层级权值的梯度值了。对于给定的样本值，神经网络通过将输出层的所有误差求平方和来计算均方误差(MSE)。

对于神经网络中给定的权值矩阵，我们必须先初始化与之对应的和权值矩阵形状相同的梯度矩阵，梯度矩阵中所有的元素都必须被初始化为。我们可以使用dim函数和matrix函数的另一种用法来实现这个初始化过程，dim函数会以向量形式返回给定矩阵的形状，如下面的代码所示：

1
2
3
4
5
(defn new-gradient-matrix
  "返回一个和给定的权值矩阵相同形状并且每一个元素都为0的矩阵。"
  [weight-matrix]
  (let [[rows cols] (dim weight-matrix)]
    (matrix 0 rows cols)))

在上面代码所定义的new-gradient-matrix函数中，matrix函数接受三个参数，一个表示每个元素内容的数值，行的大小以及列的大小去初始化一个矩阵。这个函数将会返回一个和给定权值矩阵相同形状的矩阵作为梯度矩阵的初始值。

我们现在来实现函数calc-gradients-and-error从而可以将calc-error函数作用在权值矩阵和输入样本值上。我们必须将calc-error函数作用在每一个训练样本上，并且累加每一次计算得到的梯度值和MSE值。然后我们计算这些累加值的平均值，并且返回与给定权值矩阵和样本集对应的取均值之后的梯度矩阵以及总的MSE值。我们用下面的代码来实现这个过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
(defn calc-gradients-and-error' [weights samples]
  (loop [gradients   (map new-gradient-matrix weights)
         total-error 1
         samples     samples]
    (let [[sample
           & samples']     samples
           [new-gradients
            squared-error] (calc-error weights sample)
            gradients'        (map plus new-gradients gradients)
            total-error'   (+ total-error squared-error)]
      (if (empty? samples')
        (list gradients' total-error')
        (recur gradients' total-error' samples')))))
        
(defn calc-gradients-and-error
  "Calculate gradients and MSE for sample
  set and weight matrix."
  [weights samples]
  (let [num-samples   (length samples)
        [gradients
         total-error] (calc-gradients-and-error'
                        weights samples)]
    (list
      (map #(div % num-samples) gradients)    ; gradients
      (/ total-error num-samples))))          ; MSE

上面代码中定义的calc-gradients-and-error函数依赖于calc-gradients-and-error'这个辅助函数。calc-gradients-and-error'函数一开始初始化了梯度矩阵，然后应用了calc-error函数的功能，最后将计算得到的梯度值和MSE累加并返回。calc-gradients-and-error函数只是简单的将calc-gradients-and-error'函数返回的权值矩阵和MSE处以样本的个数求取平均值。

现在，我们唯一没有实现的就是利用之前计算得到的梯度值去更新神经网络每一个节点的权值了。简单的来说，我们需要一直更新权重矩阵直到MSE能收敛到一个很小的值。这实际上是对神经网络中的每一个节点使用梯度下降算法。现在我们将会实现这个稍有不同的梯度下降算法从而可以通过连续不断地更新神经网络中节点的权值的方式来对神经网络进行训练，如下面的代码所示：

1
2
3
4
5
6
(defn gradient-descent-complete?
  "判断梯度下降训练算法是否达到可以结束的条件。"
  [network iter mse]
  (let [options (:options network)]
    (or (>= iter (:max-iters options))
        (< mse (:desired-error options)))))

上面代码定义的gradient-descent-complete?函数只是简单地检查梯度下降算法是否达到了终止条件。这个函数假设使用network参数表示的神经网络是一个带有:options键的map或者record类型的对象。这个键对应的值将会保存有神经网络中所有的配置选项。gradient-descent-complete?函数会检查神经网络总的MSE是否小于期望值或者训练的迭代次数是否已经达到了最大值，这两个条件参数分别作为:desire-error键和:max-iters键的值存储在神经网络的配置选项中。

现在，我们将会为多层感知器神经网络实现梯度下降算法。在这个实现中，我们利用梯度下降算法提供的step函数来计算权值的变化量。计算出来的权值的变化量再被加到神经网络突触现有的权值上。为多层感知器神经网络实现梯度下降算法的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
(defn apply-weight-changes
  "利用对应的变换量去更新权值矩阵。"
  [weights changes]
  (map plus weights changes))

(defn gradient-descent
  "利用梯度下降去训练调整神经网络的权值"
  [step-fn init-state network samples]
  (loop [network network
         state init-state
         iter 0]
    (let [iter     (inc iter)
          weights  (:weights network)
          [gradients
           mse]    (calc-gradients-and-error weights samples)]
      (if (gradient-descent-complete? network iter mse)
        network
        (let [[changes state] (step-fn network gradients state)
              new-weights     (apply-weight-changes weights changes)
              network         (assoc network :weights new-weights)]
          (recur network state iter))))))

上面代码定义的apply-weight-changes函数只是简单的将神经网络中的权值矩阵和其对应的变化量相加。gradient-descent函数需要一个step函数(准确的来说是step-fn函数)，神经网络权值变化量矩阵的初识状态，神经网络自身，以及用来训练神经网络的训练数据集。这个函数每次计算神经网络训练时的梯度矩阵以及权值变化矩阵，其中计算权值变化矩阵是通过step-in函数来实现的。然后使用apply-weight-changes函数来更新神经网络的权值，重复迭代这个操作过程直到gradient-descent-complete?函数返回true。神经网络的权值矩阵可以被network这个map对象的:weights键索引到。更新权值矩阵也是用新的权值矩阵去替换掉原本与:weights键对应的值。在反向传播算法中，我们需要确定神经网络的学习速率和学习动量。这两个参数需要在计算权值变化值之前被确定下来。step-fn函数可以得到这两个参数进而可以计算权值的变化量，’step-fn’函数被当做参数传给gradient-descent函数，如下面的代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
(defn calc-weight-changes
  "计算权值的变化量:
  changes = learning rate * gradients +
            learning momentum * deltas"
  [gradients deltas learning-rate learning-momentum]
  (map #(plus (mult learning-rate %1)
              (mult learning-momentum %2))
       gradients deltas))
       
(defn bprop-step-fn [network gradients deltas]
  (let [options             (:options network)
        learning-rate       (:learning-rate options)
        learning-momentum   (:learning-momentum options)
        changes             (calc-weight-changes
                              gradients deltas
                              learning-rate learning-momentum)]
    [(map minus changes) changes]))

(defn gradient-descent-bprop [network samples]
  (let [gradients (map new-gradient-matrix (:weights network))]
    (gradient-descent bprop-step-fn gradients
                      network samples)))

上面代码定义的calc-weight-changes函数利用神经网络给定层的梯度矩阵以及前一次计算得到的权值变化量矩阵计算这一次迭代权值的变化量，实际上就是上面公式提到的这一项。bprop-step-fn函数从用network表示成的神经网络对象中提取出学习速率和学习动量两个参数，然后调用calc-weight-changes函数。由于最终在grandient-descent函数中权值矩阵是会加上权值变化量矩阵，所以我们需要minus函数让权值变化矩阵中的元素取反。

gradient-descent-bprop函数只是简单的初始化了神经网络的权值变化量矩阵，然后将bprop-step-fn当做step参数传入gradient-descent函数，有了gradient-descent-bprop函数我们就可以实现之前定义的抽象协议NeuralNetwork，如下面代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
(defn round-output
  "利用四舍五入返回距离传入浮点数最近的整数"
  [output]
  (mapv #(Math/round ^Double %) output))

(defrecord MultiLayerPerceptron [options]
  NeuralNetwork

  ;; 计算给定输入的输出值
  (run [network inputs]
    (let [weights (:weights network)
          input-activations (matrix inputs)]
      (forward-propagate weights input-activations)))

  ;; 对于给定的输入将输出值映射到一个二值范围内
  (run-binary [network inputs]
    (round-output (run network inputs)))

  ;; 利用样本数据来训练多层感知器神经网络
  (train-ann [network samples]
    (let [options         (:options network)
          hidden-neurons  (:hidden-neurons options)
          epsilon         (:weight-epsilon options)
          [first-in
           first-out]     (first samples)
          num-inputs      (length first-in)
          num-outputs     (length first-out)
          sample-matrix   (map #(list (matrix (first %))
                                      (matrix (second %)))
                               samples)
          layer-sizes     (conj (vec (cons num-inputs
                                           hidden-neurons))
                                num-outputs)
          new-weights     (random-initial-weights layer-sizes epsilon)
          network         (assoc network :weights new-weights)]
      (gradient-descent-bprop network sample-matrix))))

上面代码定义的MultiLayerPerceptron类型使用gradient-descent-bprop函数来训练一个多层感知器神经网络。train-ann函数首先会从神经网络对象的配置选项中提取出隐含层节点的个数以及常数的值，神经网络各个层级的大小也绑定在了layer-sizes变量上面。然后使用random-initial-weights函数来初始化神经网络的权值矩阵，并且使用assoc函数去更新network对象中的权值矩阵。最终调用gradient-descent-bprop函数利用反向传播学习算法去训练神经网络。

使用MultiLayerPerceptron类定义的神经网络对象根据NeuralNetwork协议规定实现了两个其他的函数，run和run-binary。run函数使用forward-propagate函数利用一个训练好的神经网络和一个输入样本来计算得到输出值。run-binary函数只是简单的将run函数计算得到的输出值做了一下四舍五入的操作，从而将输出值映射到了一个二值集合上面。

一个使用MultiLayerPerceptron类定义的神经网络对象还需要一个可以用于描述神经网络所有配置选项值的options对象作为初始化参数。我们可以用下面的代码定义这个配置参数对象：

1
2
3
4
5
6
7
8
9
10
11
(def default-options
  {:max-iters 10000
   :desired-error 0.0020
   :hidden-neurons [3]
   :learning-rate 0.3
   :learning-momentum 0.01
   :weight-epsilon 5})

(defn train [samples]
  (let [network (MultiLayerPerceptron. default-options)]
    (train-ann network samples)))

default-options对象中包含了一系列用于抽象描述神经网络的配置参数，如下所示：

  • :max-iters: 这个键确定了梯度下降算法迭代的最大次数。
  • :desired-error: 这个变量确定了神经网络可以接受的MSE的阈值。
  • :hidden-neurons: 这个变量确定了神经网络中隐含层节点的个数，[3]表示了只有一个隐含层，并且这个隐含层有三个感知器节点。
  • :learning-rate与:learning-momentum: 这两个键对应的值确定了反向传播学习算法更新权值这一个步骤中的学习速率和学习动量值。
  • :epsilon: 这个变量确定了在random-initial-weights函数中初始化神经网络权值矩阵时用到的常数。

我们同样定义了一个简单的帮助函数train，这个函数会创建一个MultiLayerPerceptron类型的神经网络对象并且使用train-ann函数和用samples参数指定的样本数据来训练这个新创建的神经网络对象。现在我们可以用被sample-data变量指定的训练样本集来创建并训练一个人工神经网络了。

1
2
user> (def MLP (train sample-data))
#'user/MLP

然后我们就可以使用这个被训练好的神经网络来针对一些输入值预测输出值了。MLP变量表示的神经网络产生的结果和异或门产生的输出已经非常接近了。

1
2
3
4
user> (run-binary MLP  [0 1])
[1]
user> (run-binary MLP  [1 0])
[1]

然而，对于某一些输入来说，训练好的神经网络也可能会输出不正确的结果，如下所示：

1
2
3
4
user> (run-binary MLP  [0 0])
[0]
user> (run-binary MLP  [1 1]) ;; 产生了不正确的输
[1]

为了提高神经网络输出值的精度，我们需要实现一些措施。我们可以使用神经网络的权值去正则化计算出来的梯度值，在之前的公式中也提到了带有正则化项的损失函数。加入了正则化项可以显著地提高神经网络预测的正确性。另外我们还可以增大神经网络训练迭代的最大次数。同样的我们还可以通过适当地调整神经网络隐含层的层数，隐含层中节点的个数，学习速率和学习动量等参数来使得这个分类预测算法表现的更加优秀，读者可以自行尝试做这些修改。

Enclog这个库(https://github.com/jimpil/enclog)对Encog这个机器学习和人工神经网络算法库的一个Clojure封装。Encog库(https://github.com/encog)有两个基本的实现，一个是在JVM平台上用java实现的，另一个是在.NET平台上用c#实现的。我们可以使用Enclog库非常轻松地构建人工神经网络来解决监督学习和非监督学习问题。

要使用Enclog库，需要在Leiningen项目下的project.clj中加入如下所示的依赖代码：

[org.encog/encog-core “3.1.0”]

[enclog “0.6.3”]

注意如上面代码所示Enclog库是依赖于Encog这个Java库的。作为示例，我们需要像下面代码所示那样去修改名字空间的声明从而可以在代码中使用Enclog库中的函数：

(ns my-namespace

  (:use [enclog nnets training]))

我们可以使用Enclog库中的enclog.nnets名字空间下的neural-pattern和network函数来创建ANN对象。neural-pattern函数被用来确定ANN中的神经网络模型。network函数接受从neural-pattern函数返回的神经网络模型从而创建一个新的ANN对象。我们可以根据具体情况下要使用的神经网络模型向network函数和neural-pattern函数提供一些配置选项值。比如下面的代码就可以定义一个前馈多层感知器神经网络：

1
2
3
4
5
(def mlp (network (neural-pattern :feed-forward)
                  :activation :sigmoid
                  :input      2
                  :output     1
                  :hidden     [3]))

对于一个前馈神经网络来说，我们可以在network函数中使用:activation这个键去指定激活函数。在我们的示例中，我们使用:sigmoid作为:activation键的值去指定人工神经网络中每一个节点的激活函数为sigmoid函数。我们同样可以用:input，:output和:hidden等键去指定神经网络中输入层，输出层以及隐含层节点的个数。

我们可以使用enclog.training名字空间中的trainer和train函数以及一些样本数据去训练通过network函数创建的ANN对象。在训练神经网络的时候必须将要使用的学习算法指定为第一个参数传给trainer函数。比如要使用反向传播学习算法，那么就用:back-prop关键字来指定。trainer函数会返回一个已经包含一个我们设定的学习算法的ANN对象。然后train函数在根据ANN对象中指定好的学习算法去训练其中的神经网络，这个过程如下面代码所示：

1
2
3
4
5
(defn train-network [network data trainer-algo]
  (let [trainer (trainer trainer-algo
                         :network network
                         :training-set data)]
    (train trainer 0.01 1000 [])))

上面代码定义的train-network函数需要接受三个参数。第一个参数是利用network函数创建的ANN对象，第二个参数是用来训练神经网络的训练数据集，第三个参数是指定训练神经网络时需要使用的学习算法。在上面的代码中我们利用:network和:training-set这两个键值来确定传给trainer函数的ANN对象和训练数据集。然后train函数再利用确定好的学习算法和样本集来训练神经网络。我们可以在train函数中分别用第一个参数和第二个参数来指定学习算法的期望误差阈值以及最大迭代次数。在上面的例子中，期望误差是0.01，最大的迭代次数是1000。传给train函数的最后一个参数是一个用来指定ANN对象行为的响亮，这里我们不需要指定特定行为，所以传递一个空响亮。
利用Enclog库中的data函数，我们可以用来创建用于训练神经网络的训练数据集。比如我们可以用data函数创建一个用于解决逻辑与非门问题的训练数据集，如下面的代码所示：

1
2
3
4
(def dataset
  (let [xor-input [[0.0 0.0] [1.0 0.0] [0.0 1.0] [1.0 1.0]]
        xor-ideal [[0.0]     [1.0]     [1.0]     [0.0]]]
        (data :basic-dataset xor-input xor-ideal)))

data函数需要用数据的类型作为第一个参数，然后将训练样本集的输入值和输出值以向量的形式分别以第二个和第三个参数传入data函数。在我们的例子中，我们会使用:basic-dataset和basic参数。:basic-dataset关键字可以被用来创建训练数据集，:basic关键字怎被用来指定训练完之后使用神经网络进行分类预测时输入值的类型。

使用dataset变量指定的数据集以及train-network函数，我们就可以将上面定义的ANN对象训练成一个与非门了，如下面代码所示：

1
2
3
4
5
6
7
8
9
10
user> (def MLP (train-network mlp dataset :back-prop))
Iteration # 1 Error: 26.461526% Target-Error: 1.000000%
Iteration # 2 Error: 25.198031% Target-Error: 1.000000%
Iteration # 3 Error: 25.122343% Target-Error: 1.000000%
Iteration # 4 Error: 25.179218% Target-Error: 1.000000%
...
...
Iteration # 999 Error: 3.182540% Target-Error: 1.000000%
Iteration # 1,000 Error: 3.166906% Target-Error: 1.000000%
#'user/MLP

根据上面代码的输出，可以看到最终训练完神经网络仍然有的误差，而目标误差是，解决这个问题可以通过增大跌打次数的方式。我们现在可以利用训练好的神经网络来根据输入值进行输出分类预测值了。为了做到这一点，我们使用Java代码compute和getData方法(在Encog库中)，在clojure代码中使用这两个Java函数需要以.compute和.getData的形式来使用。我们可以定义一个帮助函数去调用.compute函数，从而可以接受一个向量形式的输入值并且得到一个二值化的分类预测输出值，如下面代码所示：

1
2
3
4
5
(defn run-network [network input]
  (let [input-data (data :basic input)
        output     (.compute network input-data)
        output-vec (.getData output)]
    (round-output output-vec)))

现在我们可以使用run-network函数和向量形式的输入值来测试训练好的神经网络，如下面代码所示：

1
2
3
4
5
6
7
8
user> (run-network MLP [1 1])
[0]
user> (run-network MLP [1 0])
[1]
user> (run-network MLP [0 1])
[1]
user> (run-network MLP [0 0])
[0]

从上面的代码中可以看到，用MLP变量表示的训练后的神经网络对于给定输入后的输出的行为和与非门完全吻合，当然适当增大训练时的最大迭代次数也可以增大分类预测的准确率。

总的来说，Enclog这个库提供给我们非常少量但是足够强大的函数来构建人工神经网络模型。在前面的例子中我们探索了前馈多层感知器神经网络模型。这个库同样提供了几个其他的神经网络模型，比如自适应共振理论神经网络(ART)，自组织映射神经网络(SOM)和艾尔曼网络。Enclog库同样允许我们去为特定的神经网络模型中的节点自定义激活函数。对于上面的前馈网络的例子，我们就是用了sigmoid函数。其他一些激活函数例如正弦函数，双曲正切函数，对数函数以及线性函数，也都可以在Enclog库中使用。Enclog库同样支持除反向传播算法以为其他多种可以用于训练神经网络的机器学习算法。

理解递归神经网络

我们现在将目光转向递归神经网络并且学习一个简单的递归神经网络模型。一个艾尔曼神经网络就是有一个输出层一个输入层一个隐含层以及一个隐含层的简单递归神经网络。当然还有一个额外的一层神经元节点作为反馈层。因为反馈层可以将之前一次迭代时隐含层的输出值作为输入传递给当前迭代时的隐含层节点，所以艾尔曼神经网络可以被用来模拟监督学习与非监督学习问题中的短期记忆效应。Enclog库中已经包好了艾尔曼神经网络的实现，下面的章节将会演示如何使用Enclog库来构建一个艾尔曼神经网络。

艾尔曼神经网络的反馈层接受来自隐含层的加权输出作为输入。在这种方式下面，神经网络可以短暂记忆之前使用隐含层生成的值，并用这些值去影响下一次预测时生成的值。因此，反馈层相当于是神经网络的一个短期记忆。一个艾尔曼神经网络可以用下图来表示：

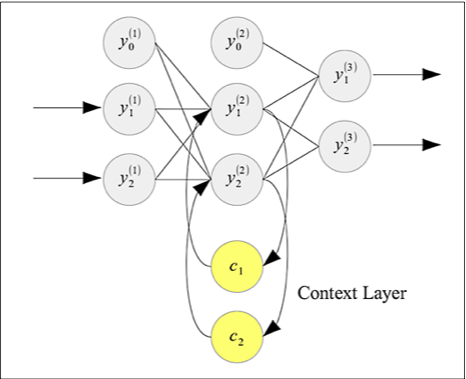
如上图所示的艾尔曼网络的整体结构酷似前馈多层感知器神经网络。艾尔曼网络只是额外地加上了一层神经元节点作为反馈层。上图所示的艾尔曼网络接受两个输入值，并且最终生成两个输入值。和多层感知器一样输入层和隐含层分别加上一个偏移量输入。隐含层神经元节点的激活值直接喂给两个反馈层的节点和。然后保存反馈层中得数据值之后会在下一次训练时作为输入传递给隐含层，从而让隐含层节点计算出新的激活值。

我们可以将:elman关键字传给Enclog库中的neural-pattern函数，从而创建一个艾尔曼网络，如下面的代码所示：

1
2
3
4
5
(def elman-network (network (neural-pattern :elman)
                             :activation :sigmoid
                             :input      2
                             :output     1
                             :hidden     [3]))

为了训练艾尔曼网络，我们需要使用弹性传播算法(更多细节可以参考Empirical Evaluation of the Improved Rprop Learning Algorithm)。这个算法同样可以被用来训练其他Enclog库支持的递归神经网络，有趣的是，弹性传播算法同样可以被用来训练前馈网络。某些情况下弹性传播算法表现出来的学习性能明显好于反向传播算法。尽管详细的解释这个算法已经超出本书的范围了，但是还是鼓励读着去详细地了解这个算法的工作原理，上面提到的那篇论文是一个不错的参考资料。可以用:resilient-prop关键字来指定之前定义过的train-network函数来使用弹性传播学习算法。在下面代码中我们使用train-network函数和dataset变量来训练艾尔曼神经网络：

1
2
3
4
5
6
7
8
9
10
user> (def EN (train-network elman-network dataset
:resilient-prop))
Iteration # 1 Error: 26.461526% Target-Error: 1.000000%
Iteration # 2 Error: 25.198031% Target-Error: 1.000000%
Iteration # 3 Error: 25.122343% Target-Error: 1.000000%
Iteration # 4 Error: 25.179218% Target-Error: 1.000000%
...
...
Iteration # 99 Error: 0.979165% Target-Error: 1.000000%
#'user/EN

如上面代码所示，弹性传播算法相对于反向传播算法达到收敛时所需要的算法迭代次数要少得多。现在我们可以像之前的例子一样将这个训练好的艾尔曼网络当做一个逻辑异或门来使用。

总的来说，递归神经网络以及弹性传播学习训练算法是利用ANNs解决分类和回归问题的另一种有效的途径。

建立自组织神经网络

自组织神经网络(SOM)是另外一种用于解决非监督学习问题的非常有趣的神经网络模型。SOMs在有许多实际的应用，比如手写字识别和图像识别。我们在第七章Clustering Data这一章讨论聚类时也会对SOMs模型进行回顾和复习。

在非监督学习领域中，训练数据集中并没有包含每一个样本的期望输出值，所以神经网络必须靠自己去从输入数据中识别和匹配训练数据中的特定模式。SOMs使用是一种竞争学习的方式，是用于解决非监督学习问题的一类特殊的学习算法，在这种方法中，神经元要相互竞争，只有获胜的一个神经元才能被激活。被激活的神经元将直接影响到神经网络最终的输出值，被激活的神经元也叫做胜利神经元。

一个自组织神经网络网络本质上是将一个高维数据映射到一个低维平面上的一个点。我们通过更新输入节点至低维平面上神经元节点的权值的方式来对自组织神经网络进行训练。SOM内部的那个低维平面一般只有一维或者二维，这个平面也成为竞争层。SOM中的神经元节点们可以根据输入值有选择地调整最终输出的模式。当SOM中一个特定的神经元被一个特定的输入模式之后，这个神经元附近的神经元也会对这个特定的输入模式产生一定的兴奋度，并且对这个模式做出相应的调整，这种神经元之间的行为也叫做横向互动。当SOM从输入数据中发现了一个特定模式之后，如果有一组具有相似模式的数据输入，SOM可以快速的识别出这个模式。自组织神经网络的结构可以用下图来描述：

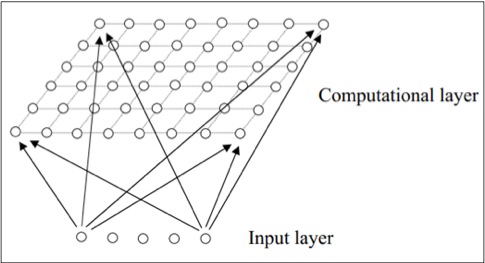
如上图所示，一个自组织神经网络由一层输入层和一层竞争层组成。自组织神经网络的竞争层也叫做特征图。输入节点将输入值映射到给竞争层的神经元节点上。在竞争层的每一个节点都可以将自己的输出乘上权值以后输入到相邻的节点上。这些权值也叫做特征图的连接权。SOM可以通过根据输入值来调整与输入节点相关联的竞争层节点的权重的方式来记住输入数据的模式。

自组织神经网络的自组织行为可以描述为如下的过程：

  1. 所有的权值都是用随机数进行初始化。
  2. 对于每一个输入模式，竞争层的节点会利用一个判别式函数去计算一个值，这些被判别式函数计算出来的值之后会被用来决定哪一个是在竞争学习中胜利的神经元节点。
  3. 判别式函数计算出来值最小的结果对应的神经元节点将会被选作胜利节点(也就是输入值向量与该输出神经元节点对应的权值向量代表的高维空间中的点的距离最近)，从输入层节点连接到这个竞争层节点的权值也会进行相应地更新，从而保证在有类似模式输入时，这个节点也最有可能在竞争学习中胜出。

为了使得有类似模式输入时，靠近胜利节点的神经元节点利用判别式函数计算出来的值也能减小，也就是这些节点也将自身向着输入模式的方向上进化，与这些节点连接的权值也需要进行更新和修改。因此胜利节点以及它附近的节点在有着相似模式的输入值输入时将会有更大的输出值或者说是激活值。通过指定训练算法中的学习速率可以调节权值的变化量，需要注意的是每一个代表输入模式的输入向量以及每一个输入神经元对应的权值向量都需要归一化，也就是向量的模长必须为1。

假设输入样本值是一个维数据，上文提到的判别式函数可以被定义为如下的形式：

在上面的等式中，这一项代表第SOM竞争层中第个神经元节点的权值向量中的第个权值。这个权值向量的长度和与这个神经元节点相连的输入层节点的个数相同。

一旦我们确定了一个在竞争学习中胜出的节点之后，我们必须选择这个胜利节点附近的神经元节点并且让他们进化。和胜利节点一样，这些选出来的节点也需要被更新权值。有很多方案可以用来选择胜利节点的邻居节点来一起进化，但是方便起见，这里只选择一个临近的节点。

一种最基本的权值更新方案就是让当前胜利节点对应的权值向量向当前的输入向量靠近，也就是让这两个向量表示的高维空间中的点的距离越来越小，这种基本的进化策略可以用如下表达式形式化地表述：

我们可以使用bubble函数，或者radial bias函数来选择胜利节点附近的一组同样需要更新权值的神经元节点(更多信息，可以参考论文Multivariable functional interpolation and adaptive networks)。

我们需要按照下面的步骤来实现学习训练算法，从而训练自组织神经网络：

  1. 用随机数初始化所有竞争层节点的的权值。
  2. 从训练数据集中选出样本数据，作为输入模式。
  3. 利用输入模式以及判别式函数来找到胜利节点。
  4. 更新胜利节点以及其附近的神经元节点的权值。
  5. 迭代2至4步，直到算法收敛。

Enclog库已经实现了自组织神经网络以及对应的训练算法。我们可以用如下代码利用Enclog库来创建并且训练一个SOM：

1
2
3
4
5
6
7
8
(def som (network (neural-pattern :som) :input 4 :output 2))

(defn train-som [data]
  (let [trainer (trainer :basic-som :network som
                         :training-set data
                         :learning-rate 0.7
                         :neighborhood-fn (neighborhood-F :single))]
    (train trainer Double/NEGATIVE_INFINITY 10 [])))

上面代码中的som变量代表一个SOM对象。train-som函数可以被用来训练SOM。:basic-som关键字用来指定训练自组织神经网络的学习训练算法。需要注意的是我们用:learning-rate键来指定学习算法的学习速率是0.7。

上面代码中传递给trainer函数的:neighborhood-fn键是用来指定对于一组输入值来说我们用哪种算法来选取自组织神经网络中与胜利节点一起进化的在胜利节点附近的节点。在代码(neighborhood-F :single)的帮助下，我们指定了只是在胜利节点附近选取一个领域节点的选取算法。当然我们也可以指定其他的领域节点选取算法，比如可以用:bubble关键字来指定使用bubble函数，使用:rbf关键字来指定使用radial basis函数。

我们可以使用train-som函数和一些输入模式来训练自组织神经网络。需要注意的是用来训练SOM的训练数据集不会包含任何输出值。自组织神经网络必须靠自己从输入数据中识别出特定的模式。一旦我们训练好了一个自组织神经网络，我们就可以使用classify这个Java方法来确定输入数据的特征了。在下面代码所示的例子中，我们仅仅提供两个输入模式来训练SOM：

1
2
3
4
5
6
7
8
9
10
(defn train-and-run-som []
  (let [input [[-1.0, -1.0, 1.0, 1.0 ]
               [1.0, 1.0, -1.0, -1.0]]
        input-data (data :basic-dataset input nil) ;数据集中没有输出值
        SOM        (train-som input-data)
        d1 (data :basic (first input))
        d2 (data :basic (second input))]
    (println "Pattern 1 class:" (.classify SOM d1))
    (println "Pattern 2 class:" (.classify SOM d2))
    SOM))

我们可以执行上面代码定义的train-and-run-som函数来观察一个自组织神经网络是如何将训练数据集中的两个输入模式识别为两个独立的类别的，代码执行的结果如下所示：

1
2
3
4
5
6
7
8
9
10
11
user> (train-and-run-som)
Iteration # 1 Error: 2.137686% Target-Error: NaN
Iteration # 2 Error: 0.641306% Target-Error: NaN
Iteration # 3 Error: 0.192392% Target-Error: NaN
...
...
Iteration # 9 Error: 0.000140% Target-Error: NaN
Iteration # 10 Error: 0.000042% Target-Error: NaN
Pattern 1 class: 1
Pattern 2 class: 0
#<SOM org.encog.neural.som.SOM@19a0818>

总的来说，自组织神经网络对于解决非监督学习问题是一个很好用的模型。而且我们还可以借助Enclog库很方便地构建自组织神经网络去对这一类问题建模分析从而解决它们。

本章概要

在这一章中，我们探索了几个有趣的人工神经网络模型。这些模型可以被用来解决监督学习和非监督学习问题。此外我们还讨论了一些其他的问题，如下所示：

  • 了解了人工神经网络的重要性以及其主要类型，例如前馈神经网络和递归神经网络。
  • 学习了多层感知器神经网络和用于训练神经网络的反向传播算法。我们通用使用Clojure和矩阵操作实现了一个简单的反向传播算法。
  • 学习使用了Enclog这个库。我们可以使用这个库来构建神经网络从而对监督学习问题和非监督学习问题进行建模。
  • 介绍了艾尔曼网络，是一种递归神经网络，可以在相对较少的迭代次数下使得训练误差很小从而使学习算法收敛。学习了使用Enclog库来构建和训练一个艾尔曼网络。
  • 介绍了自组织神经网络，可以用于解决非监督学习领域内的问题。然后学习使用Enclog库来构建并且训练一个自组织神经网络。